
期末检测卷
时间:120分钟 满分:120分
|
题号 |
一 |
二 |
三 |
总分 |
|
得分 |
|
|
|
|
一、选择题(每小题3分,共30分)
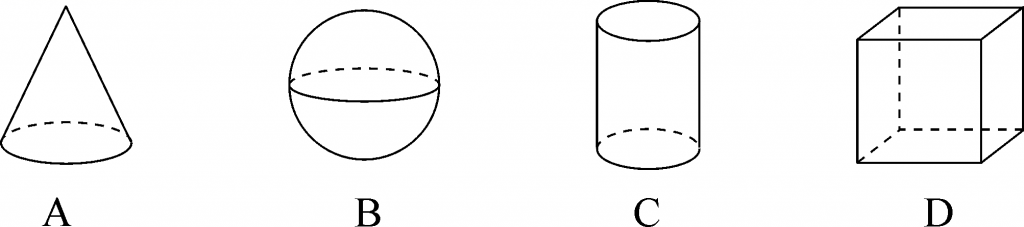
1.下列立体图形中,主视图是三角形的是( )
2.已知反比例函数y=x(k)(k>0)的图象经过点A(1,a)、B(3,b),则a与b的关系正确的是( )
A.a=b B.a=-b C.a<b D.a>b
3.如图,AD∥BE∥CF,直线l1、l2与这三条平行线分别交于点A、B、C和点D、E、F.已知AB=1,BC=3,DE=2,则EF的长为( )
A.4 B.5 C.6 D.8
第3题图 第4题图
4.△ABC在正方形网格中的位置如图所示,则cosB的值为( )
A.5(5) B.5(5) C.2(1) D.2
5.如图,放映幻灯片时通过光源把幻灯片上的图形放大到屏幕上,若光源到幻灯片的距离为20cm,到屏幕的距离为60cm,且幻灯片中的图形的高度为6cm,则屏幕上图形的高度为( )
A.6cm B.12cm C.18cm D.24cm
第5题图 第6题图
6.如图,反比例函数y1=x(k1)和正比例函数y2=k2x的图象交于A(-1,-3)、B(1,3)两点.若x(k1)>k2x,则x的取值范围是( )
A.-1<x<0 B.-1<x<1
C.x<-1或0<x<1 D.-1<x<0或x>1
7.已知两点A(5,6)、B(7,2),先将线段AB向左平移一个单位,再以原点O为位似中心,在第一象限内将其缩小为原来的2(1)得到线段CD,则点A的对应点C的坐标为( )
A.(2,3) B.(3,1) C.(2,1) D.(3,3)
8.如图,点A是反比例函数y=x(k)(x<0)的图象上的一点,过点A作平行四边形ABCD,使点B、C在x轴上,点D在y轴上.已知平行四边形ABCD的面积为6,则k的值为( )
A.6 B.-6 C.3 D.-3
第8题图 第9题图 第10题图
9.如图,小王在长江边某瞭望台D处,测得江面上的渔船A的俯角为40°.若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1∶0.75,坡长BC=10米,则此时AB的长约为(参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84)( )
A.5.1米 B.6.3米 C.7.1米 D.9.2米
10.如图,在▱ABCD中,AC,BD相交于点O,点E是OA的中点,连接BE并延长交AD于点F,已知S△AEF=4,则下列结论:①FD(AF)=2(1);②S△BCE=36;③S△ABE=12;④△AEF∽△ACD,其中一定正确的是( )
A.①②③④ B.①④ C.②③④ D.①②③
二、填空题(每小题3分,共24分)
11.若反比例函数y=x(k)的图象经过点(1,-6),则k的值为________.
12.在△ABC中,∠B=45°,cosA=2(1),则∠C的度数是________.[来源:学&科&网Z&X&X&K]
13.如图,△ABC的两条中线AD和BE相交于点G,过点E作EF∥BC交AD于点F,那么GD(FG)=________.
第13题图 第14题图 第15题图
14.如图,直线y=x+2与反比例函数y=x(k)的图象在第一象限交于点P.若OP=,则k的值为________.
15.由一些大小相同的小正方体搭成的几何体的主视图和俯视图如图所示,则搭成该几何体的小正方体最多有________个.
16.如图所示,为了测量垂直于水平地面的某建筑物AB的高度,测量人员在该建筑物附近C处,测得建筑物顶端A处的仰角为45°,随后沿直线BC向前走了100米后到达D处,在D处测得A处的仰角为30°,则建筑物AB的高度约为________米(注:不计测量人员的身高,结果按四舍五入保留整数,参考数据:≈1.41,≈1.73).
第16题图 第17题图 第18题图
17.如图所示是一块含30°,60°,90°的直角三角板,直角顶点O位于坐标原点,斜边AB垂直于x轴,顶点A在函数y1=x(k1)(x>0)的图象上,顶点B在函数y2=x(k2)(x>0)的图象上,∠ABO=30°,则k2(k1)=________.
18.如图,在▱ABCD中,∠B=30°,AB=AC,O是两条对角线的交点,过点O作AC的垂线分别交边AD,BC于点E,F,点M是边AB的一个三等分点.连接MF,则△AOE与△BMF的面积比为________.
三、解答题(共66分)
19.(6分)计算:3-2cos60°(sin45°+cos30°)-sin60°(1-sin30°).
[来源:学§科§网Z§X§X§K]
20.(8分)如图是由两个长方体组合而成的一个立体图形的三视图,根据图中所标尺寸(单位:mm),求这个立体图形的表面积.
21.(10分)如图,已知反比例函数y=x(k)(k≠0)的图象经过点B(3,2),点B与点C关于原点O对称,BA⊥x轴于点A,CD⊥x轴于点D.
(1)求这个反比函数的解析式;
(2)求△ACD的面积.
[来源:学科网ZXXK]
22.(10分)美丽的黄河宛如一条玉带穿城而过,沿河两岸的滨河路风情线是兰州最美的景观之一.数学课外实践活动中,小林在南滨河路上的A,B两点处,利用测角仪分别对北岸的一观景亭D进行了测量.如图,测得∠DAC=45°,∠DBC=65°.若AB=132米,求观景亭D到南滨河路AC的距离(结果精确到1米,参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14).
23.(10分)如图,已知四边形ABCD内接于⊙O,A是︵(BDC)的中点,AE⊥AC于A,与⊙O及CB的延长线交于点F、E,且︵(BF)=︵(AD).
(1)求证:△ADC∽△EBA;[来源:学&科&网Z&X&X&K]
(2)如果AB=8,CD=5,求tan∠CAD的值.
24.(10分)如图,直线y=ax+1与x轴、y轴分别相交于A、B两点,与双曲线y=x(k)(x>0)相交于点P,PC⊥x轴于点C,且PC=2,点A的坐标为(-2,0).
(1)求双曲线的解析式;
(2)若点Q为双曲线上点P右侧的一点,且QH⊥x轴于H,当以点Q、C、H为顶点的三角形与△AOB相似时,求点Q的坐标.
25.(12分)已知四边形ABCD的一组对边AD、BC的延长线交于点E.
(1)如图①,若∠ABC=∠ADC=90°,求证:ED·EA=EC·EB;
(2)如图②,若∠ABC=120°,cos∠ADC=5(3),CD=5,AB=12,△CDE的面积为6,求四边形ABCD的面积;
(3)如图③,另一组对边AB、DC的延长线相交于点F.若cos∠ABC=cos∠ADC=5(3),CD=5,CF=ED=n,直接写出AD的长(用含n的式子表示).
参考答案与解析
1.A 2.D 3.C 4.A 5.C 6.C 7.A 8.B 9.A
10.D 解析:在▱ABCD中,AO=2(1)AC.∵点E是OA的中点,∴AE=3(1)CE.∵AD∥BC,∴△AFE∽△CBE,∴BC(AF)=CE(AE)=3(1).∵AD=BC,∴AF=3(1)AD,∴FD(AF)=2(1),故①正确;∵S△AEF=4,S△BCE(S△AEF)=BC(AF)=9(1),∴S△BCE=36,故②正确;∵BE(EF)=CE(AE)=3(1),∴S△ABE(S△AEF)=3(1),∴S△ABE=12,故③正确;∵BF不平行于CD,∴△AEF与△ADC只有一个角相等,∴△AEF与△ACD不一定相似,故④错误,故选D.
11.-6 12.75° 13.2(1)
14.3 解析:设点P的坐标为(m,m+2).∵OP=,∴=,解得m1=1,m2=-3(不合题意,舍去),∴点P的坐标为(1,3),∴3=1(k),解得k=3.
15.7 解析:根据题意得,则搭成该几何体的小正方体最多有1+1+1+2+2=7(个).
16.137
17.-3(1) 解析:设AB交x轴于点C.∵∠ABO=30°,∴∠OAC=60°.∵AB⊥OC,∴∠ACO=90°,∴∠AOC=30°.设AC=a,则OA=2a,OC=a,∴A(a,a).∵A在函数y1=x(k1)(x>0)的图象上,∴k1=a·a=a2.在Rt△BOC中,OB=2OC=2a,∴BC==3a,∴B(a,-3a).∵B在函数y2=x(k2)(x>0)的图象上,∴k2=-3a·a=-3a2,∴k2(k1)=-3(1).
18.3∶4 解析:设AB=AC=m,则BM=3(1)m.∵O是两条对角线的交点,∴OA=OC=2(1)AC=2(1)m.∵∠B=30°,AB=AC,∴∠ACB=∠B=30°.∵EF⊥AC,∴cos∠ACB=FC(OC),即cos30°=FC(m),∴FC=3(3)m.∵AE∥FC,∴∠EAC=∠FCA,又∵∠AOE=∠COF,AO=CO,∴△AOE≌△COF,∴AE=FC=3(3)m,∴OE=2(1)AE=6(3)m,∴S△AOE=2(1)OA·OE=2(1)×2(1)m×6(3)m=24(3)m2.作AN⊥BC于N.∵AB=AC,∴BN=CN=2(1)BC.∵BN=2(3)AB=2(3)m,∴BC=m,∴BF=BC-FC=m-3(3)m=3(3)m.作MH⊥BC于H.∵∠B=30°,∴MH=2(1)BM=6(1)m,∴S△BMF=2(1)BF·MH=2(1)×3(3)m×6(1)m=18(3)m2,∴S△BMF(S△AOE)=3()=4(3).故答案为3∶4.
[来源:学科网ZXXK]
19.解:原式=2(1)-2(3)×2(1)=4(2)+4(3)-2(3)+4(3)=4(2).(6分)
20.解:根据三视图可知立体图形下面的长方体的长、宽、高分别为8mm,6mm,2mm,上面的长方体的长、宽、高分别为4mm,2mm,4mm.(3分)则这个立体图形的表面积为2(8×6+6×2+8×2)+2(4×2+2×4+4×4)-2×4×2=200(mm2).(7分)
答:这个立体图形的表面积为200mm2.(8分)
21.解:(1)将B点坐标代入y=x(k)中,得3(k)=2,解得k=6,∴反比例函数的解析式为y=x(6).(4分)
(2)∵点B与点C关于原点O对称,∴C点坐标为(-3,-2).∵BA⊥x轴,CD⊥x轴,∴A点坐标为(3,0),D点坐标为(-3,0).(7分)∴S△ACD=2(1)AD·CD=2(1)×[3-(-3)]×|-2|=6.(10分)
22.解:过点D作DE⊥AC,垂足为E.设BE=x米,在Rt△DEB中,tan∠DBE=BE(DE).∵∠DBC=65°,∴DE=xtan65°米.(3分)又∵∠DAC=45°,∴AE=DE.∴132+x=xtan65°,(6分)∴x≈115.8,∴DE≈248(米).∴观景亭D到南滨河路AC的距离约为248米.(10分)
23.(1)证明:∵四边形ABCD内接于⊙O,∴∠CDA+∠ABC=180°.又∵∠ABE+∠ABC=180°,∴∠CDA=∠ABE.(2分)∵︵(BF)=︵(AD),∴∠DCA=∠BAE.∴△ADC∽△EBA.(4分)
(2)解:∵A是︵(BDC)的中点,∴︵(AB)=︵(AC),∴AB=AC=8.(6分)∵△ADC∽△EBA,∴∠CAD=∠AEC,AB(DC)=AE(AC),∴tan∠CAD=tan∠AEC=AE(AC)=AB(DC)=8(5).(10分)
24.解:(1)把A(-2,0)代入y=ax+1中求得a=2(1),所以y=2(1)x+1,求得P点坐标为(2,2).(2分)把P(2,2)代入y=x(k)求得k=4,所以双曲线的解析式为y=x(4).(4分)
(2)设Q点坐标为(a,b).因为Q(a,b)在y=x(4)上,所以b=a(4).由y=2(1)x+1,可得B点坐标为(0,1),则BO=1.由A点坐标为(-2,0),得AO=2.当△QCH∽△BAO时,AO(CH)=BO(QH),即2(a-2)=1(b),所以a-2=2b,a-2=2×a(4),解得a=4或a=-2(舍去),所以Q点坐标为(4,1).(7分)当△QCH∽△ABO时,BO(CH)=AO(QH),即1(a-2)=2(b),所以2a-4=a(4),解得a=1+或a=1-(舍去),所以Q点坐标为(1+,2-2).综上所述,Q点坐标为(4,1)或(1+,2-2).(10分)
25.(1)证明:∵∠ADC=90°,∴∠EDC=90°,∴∠ABE=∠CDE.又∵∠AEB=∠CED,∴△EAB∽△ECD,(2分)∴ED(EB)=EC(EA),∴ED·EA=EC·EB.(4分)
(2)解:过点C作CG⊥AD于点D,过点A作AH⊥BC于点H.∵CD=5,cos∠ADC=5(3),∴DG=3,CG=4.∵S△CED=6,∴ED=3,∴EG=6.∵AB=12,∠ABC=120°,则∠BAH=30°,∴BH=6,AH=6.(6分)由(1)得△ECG∽△EAH,∴EH(EG)=AH(CG),∴EH=9,∴S四边形ABCD=S△AEH-S△ECD-S△ABH=2(1)×6×9-6-2(1)×6×6=75-18.(9分)
(3)n+6(5n+25)(12分) 解析:作CH⊥AD于H,则CH=4,DH=3.∴tanE=n+3(4).作AG⊥DF于点G.设AD=5a,则DG=3a,AG=4a,∴FG=DF-DG=5+n-3a.∵CH⊥AD,AG⊥DF,∠E=∠F,∴△AFG∽△CEH,∴FG(AG)=EH(CH),∴5+n-3a(4a)=n+3(4),∴a=n+6(n+5),∴AD=5a=n+6(5n+25).
备注:以下内容仅显示部分,需完整版请下载!











