重庆市梁平县九年级(下)期中模拟试卷
一.选择题(共10小题,满分30分)
1.若(m﹣2)x|m|+mx﹣1=0是关于x的一元二次方程,则( )
A.m=±2 B.m=2 C.m=﹣2 D.m≠±2
2.如图,四个几何体分别为长方体、圆柱体、球体和三棱柱,这四个几何体中有三个的某一种视图都是同一种几何图形,则另一个几何体是( )
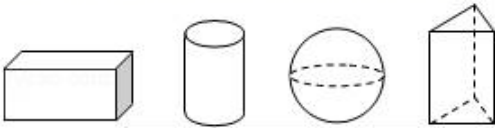
A.长方体 B.圆柱体 C.球体 D.三棱柱
3.在同一坐标系中(水平方向是x轴),函数y=和y=kx+3的图象大致是( )
A. B.
C. D.
4.在一个不透明的布袋中,红色、黑色、白色的玻璃球共有40个,除颜色外其他完全相同.小张通过多次摸球试验后发现,其中摸到红色、黑色球的频率稳定在15%和45%,则口袋中白色球的个数很可能是( )
A.6 B.16 C.18 D.24
5.已知,那么下列等式中,不成立的是( )
A. B. C. D.4x=3y
6.如图,A、B、C、P、Q、甲、乙、丙、丁都是方格纸中的格点,如果△RPQ∽△ABC,那么点R应是甲、乙、丙、丁四点中的( )
A.甲 B.乙 C.丙 D.丁
7.有一块直角边AB=3cm,BC=4cm的Rt△ABC的铁片,现要把它加工成一个正方形(加工中的损耗忽略不计),则正方形的边长为( )
A. B. C. D.
8.如图,已知点C是线段AB的黄金分割点,且BC>AC.若S1表示以BC为边的正方形面积,S2表示长为AB、宽为AC的矩形面积,则S1与S2的大小关系为( )
A.S1>S2 B.S1=S2 C.S1<S2 D.不能确定
9.某药品经过两次降价,每瓶零售价由168元降为108元,已知两次降价的百分率相同,设每次降价的百分率为x,根据题意列方程得( )
A.168(1+x)2=108 B.168(1﹣x)2=108
C.168(1﹣2x)=108 D.168(1﹣x2)=108
10.如图,在△ABC与△ADE中,∠BAC=∠D,要使△ABC与△ADE相似,还需满足下列条件中的( )
A. = B. = C. = D. =
二.填空题(共4小题,满分16分,每小题4分)
11.关于x的方程x2﹣3x+m=0有一个根是1,则方程的另一个根是 .
12.如图,四边形ABCD与四边形EFGH位似,其位似中心为点O,且=,则= .
13.如图,四边形ABCD是菱形,∠DAB=50°,对角线AC,BD相交于点O,DH⊥AB于H,连接OH,则∠DHO= 度.
14.如图,四边形OABC是矩形,四边形ADEF是正方形,点A、D在x轴的负半轴上,点C在y轴的正半轴上,点F在AB上,点B、E在反比例函数y=(k为常数,k≠0)的图象上,正方形ADEF的面积为4,且BF=2AF,则k值为 .
三.解答题(共2小题,满分18分)
15.(12分)解方程:x2﹣4=﹣3x﹣6.
16.(6分)已知y是x的反比例函数,且点A(3,5)在这个函数的图象上.
(1)求y与x之间的函数关系式;
(2)当点B(﹣5,m)也在这个反比例函数的图象上时,求△AOB的面积.
四.解答题(共4小题,满分36分)
17.(8分)在长、宽都为4m,高为3m的房间的正中央的天花板上悬挂着一只白炽灯泡,为了集中光线,加上了灯罩(如图所示).已知灯罩深AN=8cm,灯泡离地面2m,为了使光线恰好照在墙角D、E处,灯罩的直径BC应为多少?(结果保留两位小数,≈1.414)
18.(8分)现有一张演唱会的门票,小明与小华为了决定谁拿这张门票去看开幕式,小华设计了一种方案如下:如图,有A、B两个转盘,其中转盘A被分成3等份,转盘B被分成4等份,并 在每一份内标上数字.两人同时分别转动其中一个转盘,转盘停止后(当指针指在边界线上时视为无效,重转),若将A转盘指针指向的数字记为x,B转盘指针指向的数字记为y,从而确定点P的坐标为P(x,y).
(1)请用列表或画树状图的方法写出所有可能得到的点P的坐标;
(2)小华提议,在(1)的基础上,若点P落在反比例函数图象上则小明赢;否则,自己赢.你觉得小明的提议对双方公平吗?请说明理由.
19.(10分)如图,菱形ABCD的对角线AC、BD交于点O,DE∥AC,CE∥BD,求证:CD=OE.
20.(10分)如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,A、C分别在坐标轴上,点B的坐标为(4,2),直线y=﹣x+3交AB,BC分别于点M,N,反比例函数y=的图象经过点M,N.
(1)求反比例函数的解析式;
(2)若点P在y轴上,且△OPM的面积与四边形BMON的面积相等,求点P的坐标.
五.填空题(共5小题,满分20分,每小题4分)
21.关于x的一元二次方程x2+(a2﹣2a)x+a﹣1=0的两个实数根互为相反数,则a的值为 .
22.如图,四边形ABCD是菱形,AC=8,DB=6,DH⊥AB于点H,则DH= .
23.从﹣3,﹣1,0,1,3这五个数中随机抽取一个数记为a,再从剩下的四个数中任意抽取一个数记为b,恰好使关于x,y的二元一次方程组有整数解,且点(a,b)落在双曲线上的概率是 .
24.如图,在△AOB中,∠AOB=90°,点A的坐标为(4,2),BO=4,反比例函数y=的图象经过点B,则k的值为 .
25.如图,在△ABC中,D,E两点分别在边BC,AB上,DE∥AC,过点E作EF∥DC,交∠ACB的平分线于点F,连结DF,若∠EDF=∠B,且BC=4,BD=1,那么EF的长度是 .
六.解答题(共3小题,满分10分)
26.某公司经销某品牌运动鞋,年销售量为10万双,每双鞋按250元销售,可获利25%,设每双鞋的成本价为a元.
(1)试求a的值;
(2)为了扩大销售量,公司决定拿出一定量的资金做广告,根据市场调查,若每年投入广告费为x(万元)时,产品的年销售量将是原销售量的y倍,且y与x之间的关系如图所示,可近似看作是抛物线的一部分.
①根据图象提供的信息,求y与x之间的函数关系式;
②求年利润S(万元)与广告费x(万元)之间的函数关系式,并请回答广告费x(万元)在什么范围内,公司获得的年利润S(万元)随广告费的增大而增多?
(注:年利润S=年销售总额﹣成本费﹣广告费)
27.(10分)如图(1),P为△ABC所在平面上一点,且∠APB=∠BPC=∠CPA=120°,则点P叫做△ABC的费马点.
(1)如果点P为锐角△ABC的费马点,且∠ABC=60°.
①求证:△ABP∽△BCP;
②若PA=3,PC=4,则PB= .
(2)已知锐角△ABC,分别以AB、AC为边向外作正△ABE和正△ACD,CE和BD相交于P点.如图(2)
①求∠CPD的度数;
②求证:P点为△ABC的费马点.
28.菱形ABCD在平面直角坐标系中的位置如图所示,对角线AC与BD的交点E恰好在y轴上,过点D和BC的中点H的直线交AC于点F,线段DE,CD的长是方程x2﹣9x+18=0的两根,请解答下列问题:
(1)求点D的坐标;
(2)若反比例函数y=(k≠0)的图象经过点H,则k= ;
(3)点Q在直线BD上,在直线DH上是否存在点P,使以点F,C,P,Q为顶点的四边形是平行四边形?若存在,请直接写出点P的坐标;若不存在,请说明理由.
参考答案
一.选择题
1.
【解答】解:∵(m﹣2)x|m|+mx﹣1=0是关于x的一元二次方程,
∴,
解得m=﹣2.
故选:C.
2.
【解答】解:长方体、圆柱体、三棱体为柱体,它们的主视图都是矩形;球的三种视图都是圆形.
故选:C.
3.
【解答】解:A、由函数y=的图象可知k>0与y=kx+3的图象k>0一致,故A选项正确;
B、因为y=kx+3的图象交y轴于正半轴,故B选项错误;
C、因为y=kx+3的图象交y轴于正半轴,故C选项错误;
D、由函数y=的图象可知k>0与y=kx+3的图象k<0矛盾,故D选项错误.
故选:A.
4.
【解答】解:∵摸到红色球、黑色球的频率稳定在15%和45%,
∴摸到白球的频率为1﹣15%﹣45%=40%,
故口袋中白色球的个数可能是40×40%=16个.
故选:B.
5.
【解答】解:A、∵,
∴=,此选项正确,不合题意;
B、∵,
∴=﹣,此选项错误,符合题意;
C、∵,
∴=,此选项正确,不合题意;
D、∵,
∴4x=3y,此选项正确,不合题意;
故选:B.
6.
【解答】解:∵△RPQ∽△ABC,
∴,
即,
∴△RPQ的高为6.
故点R应是甲、乙、丙、丁四点中的乙处.
故选:B.
7.
【解答】解:如图,过点B作BP⊥AC,垂足为P,BP交DE于Q.
∵S△ABC=AB•BC=AC•BP,
∴BP===.
∵DE∥AC,
∴∠BDE=∠A,∠BED=∠C,
∴△BDE∽△BAC,
∴.
设DE=x,则有:,
解得x=,
故选:D.
8.
【解答】解:∵C是线段AB的黄金分割点,且BC>AC,
∴BC2=AC•AB,
∵S1表示以BC为边的正方形面积,S2表示长为AB、宽为AC的矩形面积,
∴S1=BC2,S2=AC•AB,
∴S1=S2.
故选:B.
9.
【解答】解:设每次降价的百分率为x,根据题意得:
168(1﹣x)2=108.
故选:B.
10.
【解答】解:∵∠BAC=∠D,,
∴△ABC∽△ADE.
故选:C.
二.填空题
11.
【解答】解:设方程的另一根为x,
∵关于x的方程x2﹣3x+m=0有一个根是1,
∴1+x=3,
解得,x=2;
故答案x=2.
12.
【解答】解:∵四边形ABCD与四边形EFGH位似,其位似中心为点O,且=,
∴=,
则==.
故答案为:.
13.
【解答】解:∵四边形ABCD是菱形,
∴OD=OB,∠COD=90°,
∵DH⊥AB,
∴OH=BD=OB,
∴∠OHB=∠OBH,
又∵AB∥CD,
∴∠OBH=∠ODC,
在Rt△COD中,∠ODC+∠DCO=90°,
在Rt△DHB中,∠DHO+∠OHB=90°,
∴∠DHO=∠DCO==25°,
故答案为:25.
14.
【解答】解:∵正方形ADEF的面积为4,
∴正方形ADEF的边长为2,
∴BF=2AF=4,AB=AF+BF=2+4=6.
设B点坐标为(t,6),则E点坐标(t﹣2,2),
∵点B、E在反比例函数y=的图象上,
∴k=6t=2(t﹣2),
解得t=﹣1,k=﹣6.
故答案为﹣6.
三.解答题
15.
【解答】解:x2﹣4=﹣3x﹣6,
x2+3x+2=0,
(x+2)(x+1)=0,
x+2=0,x+1=0,
x1=﹣2,x2=﹣1.
16.
【解答】解:(1)设反比例函数解析式为y=,
将点A(3,5)代入解析式得,k=3×5=15,y=.
(2)将点B(﹣5,m)代入y=得,m==﹣3,
则B点坐标为(﹣5,﹣3),
设AB的解析式为y=kx+b,
将A(3,5),B(﹣5,﹣3)代入y=kx+b得,
,
解得,,
函数解析式为y=x+1,
D点坐标为(0,1),
S△ABO=S△ADO+S△BDO=×1×3+=×1×5=4.
四.解答题
17.
【解答】解:如图,光线恰好照在墙角D、E处,AN=0.08m,AM=2m,
由于房间的地面为边长为4m的正方形,则DE=4m,
∵BC∥DE,
∴△ABC∽△ADB,
∴=,即=,
∴BC≈0.23(m).
答:灯罩的直径BC约为0.23m.
18.
【解答】解:(1)列表得:
|
|
1 |
2 |
3 |
4 |
|
1 |
(1,1) |
(1,2) |
(1,3) |
(1,4) |
|
2 |
(2,1) |
(2,2) |
(2,3) |
(2,4) |
|
4 |
(4,1) |
(4,2) |
(4,3) |
(4,4) |
则所有可能的结果共有12种;
(2)∵若P在函数上,则P为(1,4),(2,2),(4,1)共3个,
∴P(小明赢)=,P(小华赢)=,
∵,
∴不公平.
19.
【解答】证明:∵四边形ABCD是菱形,
∴∠DOC=90°,
∵DE∥AC,CE∥BD,
∴四边形CODE是矩形,
∴CD=OE.
20.
【解答】解:(1)∵B(4,2),四边形OABC是矩形,
∴OA=BC=2,
将y=2代入y=﹣x+3得:x=2,
∴M(2,2),
将x=4代入y=﹣x+3得:y=1,
∴N(4,1),
把M的坐标代入y=得:k=4,
∴反比例函数的解析式是y=;
(2)由题意可得:
S四边形BMON=S矩形OABC﹣S△AOM﹣S△CON
=4×2﹣×2×2﹣×4×1
=4;
∵△OPM的面积与四边形BMON的面积相等,
∴OP×AM=4,
∵AM=2,
∴OP=4,
∴点P的坐标是(0,4)或(0,﹣4).
五.填空题
21.
【解答】解:
∵方程x2+(a2﹣2a)x+a﹣1=0的两个实数根互为相反数,
∴a2﹣2a=0,解得a=0或a=2,
当a=2时,方程为x2+1=0,该方程无实数根,舍去,
∴a=0,
故答案为:0.
22.
【解答】解:∵四边形ABCD是菱形,
∴OA=OC=4,OB=OD=3,AC⊥BD,
在Rt△AOB中,AB==5,
∵S菱形ABCD=•AC•BD,
S菱形ABCD=DH•AB,
∴DH•5=•6•8,
∴DH=.
故答案为.
23.
【解答】解:从﹣3,﹣1,0,1,3这五个数中随机抽取一个数记为a,再从剩下的四个数中任意抽取一个数记为b,则(a,b)的所有可能性是:
(﹣3,﹣1)、(﹣3,0)、(﹣3,1)、(﹣3,3)、
(﹣1,﹣3)、(﹣1,0)、(﹣1,1)、(﹣1,3)、
(0,﹣3)、(0,﹣1)、(0,1)、(0,3)、
(1,﹣3)、(1,﹣1)、(1,0)、(1,3)、
(3,﹣3)、(3,﹣1)、(3,0)、(3,1),
将上面所有的可能性分别代入关于x,y的二元一次方程组有整数解,且点(a,b)落在双曲线上的是:(﹣3,1),(﹣1,3),(3,﹣1),
故恰好使关于x,y的二元一次方程组有整数解,且点(a,b)落在双曲线上的概率是:,
故答案为:.
24.
【解答】解:过点A作AC⊥x轴,过点B作BD⊥x轴,垂足分别为C、D,则∠OCA=∠BDO=90°,
∴∠DBO+∠BOD=90°,
∵∠AOB=90°,
∴∠AOC+∠BOD=90°,
∴∠DBO=∠AOC,
∴△DBO∽△COA,
∴==,
∵点A的坐标为(4,2),
∴AC=2,OC=4,
∴AO==2,
∴==
即BD=8,DO=4,
∴B(﹣4,8),
∵反比例函数y=的图象经过点B,
∴k的值为﹣4×8=﹣32.
故答案为﹣32
25.
【解答】解:延长EF交AC于M.设EF=m.
∵EF∥DC,
∴∠BDE=∠FED,
∵∠EDF=∠EBD,
∴△EDF∽△DBE,
∴ED2=BD•EF,
∴ED=,
∵EM∥BC,
∴∠MFC=∠FCB,
∵∠MCF=∠FCD,
∴∠MFC=∠MCF,
∴MC=FM,
∵DE∥CM,EM∥CD,
∴四边形EMCD是平行四边形,
∴CM=DE=FM=,EM=CD=3,
∴x+=3,
解得x=或(舍弃),
∴EF=,
故答案为.
六.解答题
26.
【解答】解:(1)a(1+25%)=250,
解得a=200(元).
(2)①依题意,设y与x之间的函数关系式为:y=ax2+bx+1
.
解得a=﹣0.01,b=0.2
故y=﹣0.01x2+0.2x+1
②S=(﹣0.01x2+0.2x+1)×[10×(250﹣200)]﹣x
S=﹣5x2+99x+500
当x=9.9万元时,S最大.
故当0<x<9.9时,公司获得的年利润随广告费的增大而增多.
注:0<x≤9.9,0≤x≤9.9均可.
27.
【解答】(1)证明:①∵∠PAB+∠PBA=180°﹣∠APB=60°,∠PBC+∠PBA=∠ABC=60°,∴∠PAB=∠PBC,
又∵∠APB=∠BPC=120°,
∴△ABP∽△BCP,
②解:∵△ABP∽△BCP,
∴=,
∴PB2=PA•PC=12,
∴PB=2;
故答案为:2;
(2)解:①∵△ABE与△ACD都为等边三角形,
∴∠BAE=∠CAD=60°,AE=AB,AC=AD,
∴∠BAE+∠BAC=∠CAD+∠BAC,即∠EAC=∠BAD,
在△ACE和△ABD中,
,
∴△ACE≌△ABD(SAS),
∴∠1=∠2,
∵∠3=∠4,
∴∠CPD=∠6=∠5=60°;
②证明:∵△ADF∽△CFP,
∴AF•PF=DF•CP,
∵∠AFP=∠CFD,
∴△AFP∽△CDF.
∴∠APF=∠ACD=60°,
∴∠APC=∠CPD+∠APF=120°,
∴∠BPC=120°,
∴∠APB=360°﹣∠BPC﹣∠APC=120°,
∴P点为△ABC的费马点.
28.
【解答】解:(1)x2﹣9x+18=0,
(x﹣3)(x﹣6)=0,
x=3或6,
∵CD>DE,
∴CD=6,DE=3,
∵四边形ABCD是菱形,
∴AC⊥BD,AE=EC==3,
∴∠DCA=30°,∠EDC=60°,
Rt△DEM中,∠DEM=30°,
∴DM=DE=,
∵OM⊥AB,
∴S菱形ABCD=AC•BD=CD•OM,
∴=6OM,OM=3,
∴D(﹣,3);
(2)∵OB=DM=,CM=6﹣=,
∴B(,0),C(,3),
∵H是BC的中点,
∴H(3,),
∴k=3×=;
故答案为:;
(3)①∵DC=BC,∠DCB=60°,
∴△DCB是等边三角形,
∵H是BC的中点,
∴DH⊥BC,
∴当Q与B重合时,如图1,四边形CFQP是平行四边形,
∵FC=FB,
∴∠FCB=∠FBC=30°,
∴∠ABF=∠ABC﹣∠CBF=120°﹣30°=90°,
∴AB⊥BF,CP⊥AB,
Rt△ABF中,∠FAB=30°,AB=6,
∴FB=2=CP,
∴P(,);
②如图2,∵四边形QPFC是平行四边形,
∴CQ∥PH,
由①知:PH⊥BC,
∴CQ⊥BC,
Rt△QBC中,BC=6,∠QBC=60°,
∴∠BQC=30°,
∴CQ=6,
连接QA,
∵AE=EC,QE⊥AC,
∴QA=QC=6,
∴∠QAC=∠QCA=60°,∠CAB=30°,
∴∠QAB=90°,
∴Q(﹣,6),
由①知:F(,2),
由F到C的平移规律可得P到Q的平移规律,则P(﹣﹣3,6﹣),即P(﹣,5);
③如图3,四边形CQFP是平行四边形,
同理知:Q(﹣,6),F(,2),C(,3),
∴P(,﹣);
综上所述,点P的坐标为:(,)或(﹣,5)或(,﹣).
备注:以下内容仅显示部分,需完整版请下载!











