花都区第二学期九年级期末复习
数学试卷
本试卷分选择题和非选择题两部分,共三大题25小题,共4页,满分150分,时间120分钟,可以使用计算器.
第一部分 选择题(共30分)
一、选择题(本题共10小题,每小题3分,满分30分.下面每小题给出的四个选项中,只有一个是正确的.)
1.给出四个数-1,0,3,-4, 最大的数是( )
A. B. C. D. -4
2.下面四个几何体中,左视图是四边形的几何体共有( )
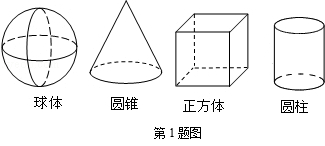
A.1个 B.2个 C.3个 D.4个
3.如图,在平面直角坐标系中,将点A(﹣2,3)向右平移3个
长度单位,那么平移后对应的点A′的坐标是( )
A.(﹣2,﹣3) B.(﹣2,6)
C.(1,3) D.(﹣2,1)
4.下列计算正确的是( ).
A.a3+a2=a5 B.(a-b)2=a2-b2 C.a6b÷a2=a3b D.(-ab3)2=a2b6
5.在某校“我的梦想”演讲比赛中,有9名学生参加决赛,他们决赛的最终成绩各不相同.其中的一名学生想要知道自己能否进入前5名,不仅要了解自己的成绩,还要了解这9名学生成绩的( ).
A.众数 B. 中位数 C.平均数 D. 方差
6.如图,菱形ABCD的两条对角线相交于O,若AC=8,BD=6,
则菱形ABCD的周长是( )
A.48 B.24 C. D.20
7.如果关于x的一元二次方程x2+px+q=0的两根分别为
,那么p,q的值分别是 ( )
8.如图,将△ABC沿直线DE折叠后,使得点B与点A重合.
已知AC=5cm,△ADC的周长为17cm,则BC的长为( )
A.12cm B.10cm C.7cm D.22cm
9.如图,AB是⊙O的直径,弦CD⊥AB,垂足为M,下列结论不成立的是( )
A.CM=DM B. C.∠ACD=∠ADC D.OM=MD
10.如图,直线y=kx+b交坐标轴于A(-2,0),B(0,3)两点,则不等式kx+b>0的解集是( )
A.x>3 B.-2<x<3
C.x<-2 D.x>-2
第二部分 非选择题(共120分)
二.填空题(本大题共6小题,每小题3分,满分18分)
11.若分式有意义,则实数x的取值范围是_____
12.拒绝“餐桌浪费”,刻不容缓.据统计全国每年浪费食物总量约50 000 000 000千克,这个数据用科学计数法表示为
13.从某班全体学生中任意选取一名男生的概率为,则该班男、女学生的比为________
14.分解因式: .
15.如图,四个边长为1的小正方形拼成一个大正方形,A、B、O
是小正方形顶点,A、B、P是⊙O上的点,则.
16.如图,Rt△ABC中,∠ACB=90°,∠ABC=60°,BC=2cm,D为BC的中点,若动点E以1cm/s的速度从A点出发,沿着A→B的方向运动,设E点的运动时间为t秒,连接DE,当△BDE是直角三角形时,t的值为
三.解答题(本大题共9小题,满分102分,解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分9分)
(1)解不等式:
(2)若(1)中的不等式的最小整数解是关于的方程的解,求
18.(本小题满分9分)已知:如图,在△ABC中,∠A=30°,∠B=60°,E为AB的中点。
(1)作∠B的平分线BD,交AC于点D;(要求:尺规作图,
保留作图痕迹,不必写作法和证明);
(2)连接DE,求证:△ADE≌△BDE。
19.(本小题满分10分)
先化简:,然后从中选择一个合适的数代入求值。
20.(本小题满分10分)某中学九(1)班为了了解全班学生喜欢球类活动的情况,采取全面调查的方法,从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好,根据调查的结果组建了4个兴趣小组,并绘制成如图所示的两幅不完整的统计图(如图①,②,要求每位学生只能选择一种自己喜欢的球类),请你根据图中提供的信息解答下列问题:
(1)九(1)班的学生人数为 ,并把条形统计图补充完整;
(2)扇形统计图中m= ,n= ,表示“足球”的扇形的圆心角是 度;
(3)排球兴趣小组4名学生中有3男1女,现在打算从中随机选出2名学生参加学校的排球队,请用列表或画树状图的方法求选出的2名学生恰好是1男1女的概率.
21.(本小题满分12分)
如图,已知菱形ABCD的对角线相交于点O,延长AB
至点E,使BE=AB,连结CE.
(1)求证:BD=EC;
(2)若AC=2, ,求菱形ABCD的面积.
22.(本小题满分12分)
马航MH370 客机“失联”,我国“海巡01号”前往搜寻。如图某天上午9时,“海巡01号” 轮船位于A处,观测到某小岛P位于轮船的北偏西67.5°,轮船以21海里/时的速度向正北方向行驶,下午2时该船到达B处,这时观测到小岛P位于该船的南偏西30°方向,求此时轮船所处位置B与小岛P的距离?(精确到0.1)
23.(本小题满分12分)
如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标为(4,2).过点D(0,3)和E(6,0)的直线分别与AB,BC交于点M,N.
(1)求直线DE的解析式和点M的坐标;
(2)若反比例函数(x>0)的图象经过点M,求该反比例函数的解析式,并通过计算判断点N是否在该函数的图象上;
(3)若反比例函数(x>0)的图象与△MNB有公共点,请直接写出m的取值范围.
24.(本小题满分14分)
如图,已知:正方形ABCD中,AB=8,点O为边AB上一动点,以点O为圆心,OB为半径的⊙O交边AD于点E(不与点A、D重合),EF⊥OE交边CD于点F.设BO=x,AE=y.
(1)求y关于x的函数关系式,并写出x的取值范围;
(2)在点O运动的过程中,△EFD的周长是否发生变化?如果发生变化,请用x的代数式表示△EFD的周长;如果不变化,请求出△EFD的周长;
(3)以点A为圆心,OA为半径作圆,在点O运动的过程中,讨论⊙O与⊙A的位置关系,并写出相应的x的取值范围.
25.(本小题满分14分)
如图,已知抛物线经过点C(-2,6),
与x轴相交于A、B两点(A在B的左侧),与y轴交于点D.
(1)求点A的坐标;
(2)设直线BC交y轴于点E,连接AE、AC,
求证:是等腰直角三角形;
(3)连接AD交BC于点F,试问当时,在抛物线上是否存在一点P使得以A、B、P为顶点的三角形与相似?若存在, 请求出点P的坐标;若不存在,请说明理由.
数学试卷参考答案
一、 选择题
CBCD BDBA DD
二、 填空题
|
题号 |
11 |
12 |
13 |
14 |
15 |
16 |
|
答案 |
|
|
4:3 |
|
1 |
2或3.5 |
三、 解答题
17、(本小题满分9分)
————————5分
—————— 7分
当时,则有—————— 8分
—————— 9分
18、(本小题满分9分)
解:(1)作出∠B的平分线BD; (图略) —————— 4分
(2)证明:∵∠ABD=×60°=30°,∠A=30°—————— 5分
∴∠ABD=∠A —————— 6分
又∵∠AED=∠BED=90°,DE=DE
∴△ADE≌△BDE —————— 9分
19、(本小题满分10分)
——————2分
—————— 3分
=— ————— 4分
= —————— 5分
= —————— 7分
∵ ∴可以取 —————— 9分
∴原式可以等于—————— 10分
20.(本小题满分10分
解:(1)九(1)班的学生人数为:12÷30%=40(人),—————— 1分
喜欢足球的人数为:40﹣4﹣12﹣16=40﹣32=8(人),—————— 3分
补全统计图如图所示;
(2)∵×100%=10%,
×100%=20%,
∴m=10,n=20,
表示“足球”的扇形的圆心角是20%×360°=72°;
故答案为:(1)40;(2)10;20;72;—————— 6分
(3)根据题意画出树状图如下:
一共有12种情况,恰好是1男1女的情况有6种,—————— 8分
所以,P(恰好是1男1女)==.—————— 10分
21.(本小题满分12分)
解:(1)∵四边形ABCD为菱形
∴AB∥CD, AB=CD —————— 2分
∵BE=AB
∴BE∥CD且BE=CD —————— 3分
∴四边形BECD为平行四边形———5分
∴DB=CE —————— 6分
(2)∵四边形BECD为平行四边形
∴DB∥CE
∴∠E=∠OBA
∴ —————— 7分
∵四边形ABCD为菱形
∴∠AOB=90°, —————— 8分
∴ —————— 9分
—————— 10分
—————— 11分
—————— 12分
22.(本小题满分12分)
解:过点P作PC⊥AB,垂足为C,设PC=x海里.—————— 1分
在Rt△APC中,∵tan∠A=,
∴AC=.—————— 4分
在Rt△PCB中,∵tan∠B=,
∴BC=.—————— 6分
∵AC+BC=AB=21×5,
∴,—————— 8分
解得. —————— 9分
∵,
∴(海里).—————— 11分
∴向阳号轮船所处位置B与城市P的距离为100海里.—————— 12分
23.(本小题满分12分)
如图,在直角坐标系中,矩形OABC的顶点O与坐标原点重合,顶点A,C分别在坐标轴上,顶点B的坐标为(4,2).过点D(0,3)和E(6,0)的直线分别与AB,BC交于点M,N.
(1)求直线DE的解析式和点M的坐标;
(2)若反比例函数(x>0)的图象经过点M,求该反比例函数的解析式,并通过计算判断点N是否在该函数的图象上;
(3)若反比例函数(x>0)的图象与△MNB有公共点,请直接写出m的取值范围.
解:(1)设直线DE为 ——————1分
∴ ,
∴ —————— 2分
∴ —————— 3分
∵B的坐标为(4,2).
∴当, —————— 4分
∴M的坐标为(2,2)——————5分
(2)∵反比例函数(x>0)的图象经过点M,
, —————— 6分
—————— 7分
—————— 8分
∴点N在反比例函数的图象上。—————— 9分
(3)m的取值范围为: —————— 12分
24.(本小题满分14分)
解:(1)∵以点O为圆心,OB为半径的⊙O交边AD于点E,
∴OB=OE,—————— 1分
∵四边形ABCD是正方形,
∴∠A=90°, ∴AO2+AE2=OE2,即(8-x)2+y2=x2,—————— 3分
∵y>0, ∴ —————— 4分
(2)△EFD的周长不变.—————— 5分
理由如下:
∵EF⊥OE, ∴∠AEO+∠DEF=90°,
∵∠D=∠A=90°,∴∠AEO+∠AOE=90°—————— 6分,
∴∠DEF=∠AOE,
∴△AOE∽△DEF,—————— 7分
∴= —————— 8分
∴=16 —————— 9分
(3)设⊙O的半径R1=x,则⊙A的半径R2=8-x,圆心距d=OA=8-x,
∵4<x<8, ∴R1>R2,
因为点A始终在⊙O内,所以外离和外切都不可能;
① 当⊙O与⊙A相交时,R1-R2<d<R1+R2,即x-8+x<8-x<x+8-x,—————— 10分
解得: —————— 11分
故可得此时:
②当⊙O与⊙A内切时,d=R1-R2,即8-x=x-8+x,
解得:x= —————— 12分
③当⊙O与⊙A内含时,0<d<R1-R2,即0<8-x<x-8+x,—————— 13分
解得: —————— 14分
25.(本小题满分14分)
解:(1)∵抛物线经过点C(-2,6)
∴
∴ —————— 1分
∴ —————— 2分
∴当,
, —————— 4分
——————4分
(2)证明:设直线BC的函数解析式为y=kx+b,
由题意得: ,解得:。
∴直线BC的解析式为y=-2x+2. —————— 5分
∴点E的坐标为(0,2)。
∴。
∴AE=CE。—————— 7分
又∵
∴ —————— 8分
∴△AEC为等腰直角三角形—————— 9分
(3)在抛物线上是否存在一点P使得以A、B、P为顶点的三角形与相似。—————— 10分
理由如下:
设直线AD的解析式为y=k1x+b1,则 ,解得:。
∴直线AD的解析式为y=x+4。
联立直线AD与直线BC的函数解析式可得:,解得:。
∴点F的坐标为( )。
则。
又∵AB=5,,
∴。 ∴。
又∵∠ABF=∠CBA,∴△ABF∽△CBA。
∴当点P与点C重合时,以A、B、P为顶点的三角形与相似。—————— 12分
又∵抛物线关于直线对称
当点P与点C的对称点重合时,以A、B、P为顶点的三角形也与相似。
∴当点P的坐标为(-2,6)或(-时,以A、B、P为顶点的三角形也与相似。
—————— 14分
备注:以下内容仅显示部分,需完整版请下载!











