
九年级(下)第四次月考数学试卷
一、选择题(共10小题,每小题3分,共30分)
1.(3分)实数+1的值在( )之间.
A.0~1 B.1~2 C.2~3 D.3~4
2.(3分)使分式有意义的x的取值范围是( )
A.x>﹣2 B.x<2 C.x≠2 D.x≠﹣2
3.(3分)运用乘法公式计算(2+a)(a﹣2)的结果是( )
A.a2﹣4a﹣4 B.a2﹣2a﹣4 C.4﹣a2 D.a2﹣4
4.(3分)下列事件是随机事件的是( )
A.任意画一个平行四边形,它是中心对称图形
B.方程x2﹣2x﹣1=0必有实数根
C.掷两次骰子,骰子向上的一面的点数之积为14
D.李老师购买了1张彩票,正好中奖
5.(3分)下列计算正确的是( )
A.x6÷x2=x3 B.2x•x=2x2 C.3x2﹣2x3=x2 D.x2+x2=2x4
6.(3分)如图,菱形ABCD中,AB∥y轴,且B(﹣10,1)、C(2,6),则点A的坐标为( )
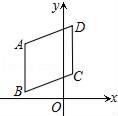
A.(﹣10,12) B.(﹣10,13) C.(﹣10,14) D.(2,12)
7.(3分)如图,几何体上半部分为正方体,下半部分为圆柱,其左视图为( )
A. B. C. D.
8.(3分)二中广雅管乐队队员的年龄,经统计有12、13、14、15四种年龄,统计结果如图.根据图中信息可以判断该批队员的年龄的众数和中位数为( )
A.8和6 B.15和14 C.8和14 D.15和13.5
9.(3分)在平面直角坐标系中,对于点P(x,y),我们把点P′(﹣y+1,x+1)叫做点P的伴随点.已知点A1的伴随点为A2, A2的伴随点为A3…,这样依次得到点A1、A2、A3、An、….若点A1(2,2),则点A2016的坐标为( )
A.(﹣2,0) B.(﹣1,3) C.(1,﹣1) D.(2,2)
10.(3分)如图,AC⊥BC,AC=BC,点D是AB中点,过C、D的⊙O交AC、BC分别于E、F.若⊙O的半径为,AC=2+2,则△CEF的面积为( )
A. B. C. D.
二、填空题(本大题共6个小题,每小题3分,共18分)
11.(3分)计算:﹣10﹣6的结果为 .
12.(3分)2016年湖北武汉中考报名人数为6.3万人,普通高中招生计划约为3.48万人,数34800用科学记数法表示为 .
13.(3分)武汉二中广雅中学开展“广学雅行”活动,从学生会“监察部”的三名学生干部(2男1女)中随机选两名进行活动督查,恰好选中两名男学生的概率是 .
14.(3分)如图,将矩形ABCD沿BD翻折,点C落在P点处,连结AP.若∠ABP=26°,那么∠APB= .
15.(3分)如图,点C是线段AB上的动点,分别以AC、BC为边在AB的同侧作等边△ACD、等边△BCE,BD、AE交于点P.若AB=6,则PC的最大值为 .
16.(3分)已知函数y=,将此函数的图象记为P.若直线y=x+b与图形P恰有两个公共点,则b的值为 .
三、解答题(共8题,共72分)
17.(8分)解方程:3x﹣1=2(x﹣2)
18.(8分)如图,四边形ABCD中,AB=AD,BC=CD,连结AC、BD交于点P,求证:AC⊥BD.
19.(8分)武汉二中广雅中学为了了解全校学生的课外阅读的情况,随机抽取了部分学生进行阅读时间调查,现将学生每学期的阅读时间m分成A、B、C、D四个等级(A等:90≤m≤100,B等:80≤m<90,C等:60≤m<80,D等:m<60;单位:小时),并绘制出了如图的两幅不完整的统计图,根据以上信息,回答下列问题:
(1)C组的人数是 人,并补全条形统计图.
(2)本次调查的众数是 等,中位数落在 等.
(3)国家规定:“中小学每学期的课外阅读时间不低于60小时”,如果该校今年有3500名学生,达到国家规定的阅读时间的人数约有 人.
20.(8分)已知双曲线y=和直线y=kx+4.
(1)若直线y=kx+4与双曲线y=有唯一公共点,求k的值.
(2)若直线y=kx+4与双曲线交于点M(x1,y1),N(x2,y2).当x1>x2,请借助图象比较y1与y2的大小.
21.(8分)如图,⊙O的直径AB⊥弦CD,垂足为点E,点P在优弧CAD上(不包含点C和点D),连PC、PD、CB,tan∠BCD=
(1)求证:AE=CD;
(2)求sin∠CPD.
22.(10分)如图所示,学校准备修建一个含内接矩形的菱形花坛(花坛为轴对称图形).矩形的四个顶点分别在菱形四条边上,菱形的高AM=3米,∠ABC=60°.设AE=x米(1≤x≤2),矩形EFGH的面积为S米2.
(1)求S与x的函数关系式;
(2)学校准备在矩形内种植红色花草,在四个三角形内种植绿色花草.已知:红色和绿色植物的价格为200元/米2,100元/米2,当x为何值时,购买花卉所需的总费用最低,并求出最低总费用(结果保留根号).
23.(10分)如图,在矩形ABCD中,E为CD的中点,F为BE上的一点,连结CF并延长交AB于点M,MN⊥CM交射线AD于点N.
(1)当F为BE中点时,求证:AM=CE;
(2)若==2,求的值;
(3)若==n,当n为何值时,MN∥BE?
24.(12分)如图1,抛物线y=﹣x2+6x与x轴交于O、A两点,点P在抛物线上,过点P的直线y=x+m与抛物线的对称轴交于点Q.
(1)这条抛物线的对称轴是:直线 ,直线PQ与x轴所夹锐角的度数是 度;
(2)若S△POQ:S△PAQ=1:2,求此时的点P坐标;
(3)如图2,点M(1,5)在抛物线上,以点M为直角顶点作Rt△MEF,且E、F均在抛物线上,则所有满足条件的直线EF必然经过定点N,求点N坐标.
参考答案与试题解析
一、选择题(共10小题,每小题3分,共30分)
1.(3分)实数+1的值在( )之间.
A.0~1 B.1~2 C.2~3 D.3~4
【解答】解:∵1<3<4,
∴1<<2,
∴2<+1<3.
故选:C.
2.(3分)使分式有意义的x的取值范围是( )
A.x>﹣2 B.x<2 C.x≠2 D.x≠﹣2
【解答】解:∵分式有意义,
∴x+2≠0,即x≠﹣2.
故选:D.
3.(3分)运用乘法公式计算(2+a)(a﹣2)的结果是( )
A.a2﹣4a﹣4 B.a2﹣2a﹣4 C.4﹣a2 D.a2﹣4
【解答】解:原式=a2﹣4,
故选:D.
4.(3分)下列事件是随机事件的是( )
A.任意画一个平行四边形,它是中心对称图形
B.方程x2﹣2x﹣1=0必有实数根
C.掷两次骰子,骰子向上的一面的点数之积为14
D.李老师购买了1张彩票,正好中奖
【解答】解:任意画一个平行四边形,它是中心对称图形是必然事件;
方程x2﹣2x﹣1=0必有实数根是必然事件;
掷两次骰子,骰子向上的一面的点数之积为14是不可能事件;
李老师购买了1张彩票,正好中奖是随机事件,
故选:D.
5.(3分)下列计算正确的是( )
A.x6÷x2=x3 B.2x•x=2x2 C.3x2﹣2x3=x2 D.x2+x2=2x4
【解答】解:A、x6÷x2=x4,故此选项错误;
B、2x•x=2x2,故此选项正确;
C、3x2与﹣2x3不是同类项,不能合并,故此选项错误;
D、x2+x2=2x2,故此选项错误;
故选:B.
6.(3分)如图,菱形ABCD中,AB∥y轴,且B(﹣10,1)、C(2,6),则点A的坐标为( )
A.(﹣10,12) B.(﹣10,13) C.(﹣10,14) D.(2,12)
【解答】解:∵B(﹣10,1)、C(2,6),
∴BC==13,
∵四边形ABCD是菱形,
∴AB=BC=13,
∴点A坐标为(﹣10,14),
故选:C.
7.(3分)如图,几何体上半部分为正方体,下半部分为圆柱,其左视图为( )
A. B. C. D.
【解答】解:从左边看下边是一个较大的矩形,上边是两个较小的矩形,
故选:D.
8.(3分)二中广雅管乐队队员的年龄,经统计有12、13、14、15四种年龄,统计结果如图.根据图中信息可以判断该批队员的年龄的众数和中位数为( )
A.8和6 B.15和14 C.8和14 D.15和13.5
【解答】解:15岁的队员最多,是8人,
所以,众数是15岁,
20人中按照年龄从小到大排列,第10、11两人的年龄都是14岁,
所以,中位数是14岁.,
故选:B.
9.(3分)在平面直角坐标系中,对于点P(x,y),我们把点P′(﹣y+1,x+1)叫做点P的伴随点.已知点A1的伴随点为A2,A2的伴随点为A3…,这样依次得到点A1、A2、A3、An、….若点A1(2,2),则点A2016的坐标为( )
A.(﹣2,0) B.(﹣1,3) C.(1,﹣1) D.(2,2)
【解答】解:观察,发现规律:A1(2,2),A2(﹣1,3),A3(﹣2,0),A4(1,﹣1),A5(2,2),…,
∴A4n+1(2,2),A4n+2(﹣1,3),A4n+3(﹣2,0),A4n+4(1,﹣1)(n为自然数).
∵2016=503×4+4,
∴点A2016的坐标为(1,﹣1).
故选:C.
10.(3分)如图,AC⊥BC,AC=BC,点D是AB中点,过C、D的⊙O交AC、BC分别于E、F.若⊙O的半径为,AC=2+2,则△CEF的面积为( )
A. B. C. D.
【解答】解:连接CD、ED、DF、EF,如右图所示,
∵AC⊥BC,AC=BC,点D是AB中点,
∴CD=DA=DB,∠CDB=90°,∠ECD=∠FBD=45°,
又∵EF是⊙O的直径,
∴∠EDF=90°,
∴∠EDC+∠CDF=∠CDF+∠FDB=90°,
∴∠EDC=∠FDB,
在△EDC和△FDB中,
,
∴△EDC≌△FDB(ASA),
∴CE=BF,
又∵AC=BC,AC=2+2,
∴BC=2+2,
即BF+FC=2+2,
∴CF+CE=2+2,
又∵∠ECF=90°,⊙O的半径为,
∴CE2+CF2=EF2,EF=2,
解得,CE•CF=4,
∴△CEF的面积为:,
故选:B.
二、填空题(本大题共6个小题,每小题3分,共18分)
11.(3分)计算:﹣10﹣6的结果为 ﹣16 .
【解答】解:﹣10﹣6=﹣16.
故﹣10﹣6的结果为﹣16.
故答案为:﹣16.
12.(3分)2016年湖北武汉中考报名人数为6.3万人,普通高中招生计划约为3.48万人,数34800用科学记数法表示为 3.48×104 .
【解答】解:34800用科学记数法表示为:3.48×104.
故答案为:3.48×104.
13.(3分)武汉二中广雅中学开展“广学雅行”活动,从学生会“监察部”的三名学生干部(2男1女)中随机选两名进行活动督查,恰好选中两名男学生的概率是 .
【解答】解:画树状图为:
共有6种等可能的结果数,其中恰好选中两名男学生的结果数为2,
所以恰好选中两名男学生的概率==.
故答案为.
14.(3分)如图,将矩形ABCD沿BD翻折,点C落在P点处,连结AP.若∠ABP=26°,那么∠APB= 32° .
【解答】解:∵△BDC与△BDE关于BD对称,
∴△BDC≌△BDP,
∴BP=BC,DP=DC,∠DBP=∠DBC.
∵四边形ABCD是矩形,
∴AB=CD=DP,AD=BC=BP,AD∥BC,
∴∠ADB=∠CBD,
∴∠PBD=∠ADB,
∴BF=DF,
∴BP﹣BF=AD﹣DF,
∴AF=PF,
∴∠FAP=∠FPA,
∵∠AFP=∠BFD,
∴2∠PAF=2∠ADB,
∴∠PAF=∠ADB,
∴AP∥BD,
∴∠APB=∠PBD,
∵∠ABP=26°,
∴∠CBD=∠DBP=(90°﹣26°)=32°,
则∠APB=32°.
故答案为:32°.
15.(3分)如图,点C是线段AB上的动点,分别以AC、BC为边在AB的同侧作等边△ACD、等边△BCE,BD、AE交于点P.若AB=6,则PC的最大值为 .
【解答】解:如图,∵△ACD与△BCE都为等边三角形,
∴AC=CD,CB=CE,∠ACD=∠BCE=60°,
∴∠ACD+∠DCE=∠BCE+∠DCE,即∠ACE=∠DCB,
在△ACE和△DCB中,
,
∴△ACE≌△DCB(SAS)
∴AE=BD;
过C作CG⊥AE,CH⊥BD,
∵△ACE≌△DCB,
∴S△ACE=S△DCB,即AE•CG=BD•CH,
∵AE=BD,
∴CG=CH,
∴KC平分∠AKB,∵∠CDB=∠EAC,
∴∠ACP=∠DPA=60°,
∴∠APB=120°,∠APQ=∠BPQ=60°,
作△APB的外接圆,延长PC交△APB的外接圆于Q,
∵∠APB=120°是定值,∠APQ=∠BPQ=60°,
∴QA=QB,点Q是定点,
∴当PQ⊥AB时,PC的长最大,
此时PA=PB,AC=BC,PC=AC•tan30°=3×=.
故答案为.
16.(3分)已知函数y=,将此函数的图象记为P.若直线y=x+b与图形P恰有两个公共点,则b的值为 0或 .
【解答】解:当直线y=x+b与y=﹣x2+2x(x≥0)有一个交点,与y=x2﹣2x(x<0)有一个交点时,
﹣x2+2x=x+b,
则x2﹣x+b=0,
△=(﹣1)2﹣4×1×b=0,得b=,
当直线y=x+b与y=﹣x2+2x(x≥0)有两个交点,与y=x2﹣2x(x<0)没有交点时,
则b=0,
故答案为:0或.
三、解答题(共8题,共72分)
17.(8分)解方程:3x﹣1=2(x﹣2)
【解答】解:去括号得:3x﹣1=2x﹣4,
解得:x=﹣3.
18.(8分)如图,四边形ABCD中,AB=AD,BC=CD,连结AC、BD交于点P,求证:AC⊥BD.
【解答】证明:在△ABC和△ADC中,
,
∴△ABC≌△ADC(SSS),
∴∠BAP=∠DAP,
∵AB=AD,
∴AC⊥BD.
19.(8分)武汉二中广雅中学为了了解全校学生的课外阅读的情况,随机抽取了部分学生进行阅读时间调查,现将学生每学期的阅读时间m分成A、B、C、D四个等级(A等:90≤m≤100,B等:80≤m<90,C等:60≤m<80,D等:m<60;单位:小时),并绘制出了如图的两幅不完整的统计图,根据以上信息,回答下列问题:
(1)C组的人数是 50 人,并补全条形统计图.
(2)本次调查的众数是 100 等,中位数落在 C 等.
(3)国家规定:“中小学每学期的课外阅读时间不低于60小时”,如果该校今年有3500名学生,达到国家规定的阅读时间的人数约有 2975 人.
【解答】解:(1)调查的总人数40÷20%=200人,C组的人数=200﹣40﹣100﹣10=50,
补充如图;
(2)本次调查的众数是 100,即B等,中位数是=75,落在C等;
(3)3500×=2975人,
答:该校今年有3500名学生,达到国家规定的阅读时间的人数约有2975人.
20.(8分)已知双曲线y=和直线y=kx+4.
(1)若直线y=kx+4与双曲线y=有唯一公共点,求k的值.
(2)若直线y=kx+4与双曲线交于点M(x1,y1),N(x2,y2).当x1>x2,请借助图象比较y1与y2的大小.
【解答】解:(1)
把①代入②得: =kx+4,
kx2+4x﹣6=0,
∵直线y=kx+4与双曲线y=有唯一公共点,
∴方程kx2+4x﹣6=0有唯一一个解,
即△=42﹣4k•(﹣6)=0,
解得:k=﹣;
(2)当x1>x2>0时,y1<y2;
当x2<x1<0时,y1<y2;
当x2<0<x1时,y1>y2.
21.(8分)如图,⊙O的直径AB⊥弦CD,垂足为点E,点P在优弧CAD上(不包含点C和点D),连PC、PD、CB,tan∠BCD=
(1)求证:AE=CD;
(2)求sin∠CPD.
【解答】(1)证明:连接AD,
∴∠BAD=∠BCD,
∵tan∠BCD=,
∴tan∠BAD=,
∴=,
∴DE=AE,
∵⊙O的直径AB⊥弦CD,垂足为点E,
∴CE=DE=CD,
∴AE=CD;
(2)解:作直径CE,连接ED,
∴∠CDE=90°,
∵tan∠BCD=,AB⊥弦CD,
∴CE=2BE,
∵AE=CD,
∴AB=CD,
∴=,
∵CE=AB,
∴=,
∴sin∠CED=,
∵∠CED=∠CPD,
∴sin∠CPD=.
22.(10分)如图所示,学校准备修建一个含内接矩形的菱形花坛(花坛为轴对称图形).矩形的四个顶点分别在菱形四条边上,菱形的高AM=3米,∠ABC=60°.设AE=x米(1≤x≤2),矩形EFGH的面积为S米2.
(1)求S与x的函数关系式;
(2)学校准备在矩形内种植红色花草,在四个三角形内种植绿色花草.已知:红色和绿色植物的价格为200元/米2,100元/米2,当x为何值时,购买花卉所需的总费用最低,并求出最低总费用(结果保留根号).
【解答】解:(1)连接AC、BD,
∵花坛为轴对称图形,
∴EH∥BD,EF∥AC,
∴△BEF∽△BAC,
∵四边形ABCD是菱形,
∴AB=BC,
又∵∠ABC=60°,
∴△ABC是等边三角形.
同理,得到△BEF是等边三角形,
∵AB==2,
∴EF=BE=AB﹣AE=(2﹣x)m,
在Rt△AEM中,∠AEM=∠ABD=30°,
则EM=AEcos∠AEM=x,
∴EH=2EM=x,
故可得S=x(2﹣x)=﹣x2+6x;
(2)∵菱形ABCD的面积为2×3=6,
矩形EFGH的面积为﹣x2+6x,
∴四个三角形的面积为6+x2﹣6x,
设总费用为W,
则W=200(﹣x2+6x)+100(6+x2﹣6x)
=﹣100x2+600x+600
=﹣100(x﹣)2+900,
∵1≤x≤2,
∴当x=时,W取得最大值,最大值为900,
答:当x=时,购买花卉所需的总费用最低,最低总费用900.
23.(10分)如图,在矩形ABCD中,E为CD的中点,F为BE上的一点,连结CF并延长交AB于点M,MN⊥CM交射线AD于点N.
(1)当F为BE中点时,求证:AM=CE;
(2)若==2,求的值;
(3)若==n,当n为何值时,MN∥BE?
【解答】解:(1)当F为BE中点时,如图1,则有BF=EF.
∵四边形ABCD是矩形,
∴AB=DC,AB∥DC,
∴∠MBF=∠CEF,∠BMF=∠ECF.
在△BMF和△ECF中,
,
∴△BMF≌△ECF,
∴BM=EC.
∵E为CD的中点,
∴EC=DC,
∴BM=EC=DC=AB,
∴AM=BM=EC;
(2)如图2所示:设MB=a,
∵四边形ABCD是矩形,
∴AD=BC,AB=DC,∠A=∠ABC=∠BCD=90°,AB∥DC,
∴△ECF∽△BMF,
∴==2,
∴EC=2a,
∴AB=CD=2CE=4a,AM=AB﹣MB=3a.
∵=2,
∴BC=AD=2a.
∵MN⊥MC,
∴∠CMN=90°,
∴∠AMN+∠BMC=90°.
∵∠A=90°,
∴∠ANM+∠AMN=90°,
∴∠BMC=∠ANM,
∴△AMN∽△BCM,
∴=,
∴=,
∴AN=a,ND=AD﹣AN=2a﹣a=a,
∴==3;
(3)当==n时,如图3:设MB=a.
∵△MFB∽△CFE,
∴=,即,解得EC=an.
∴AB=2an.
又∵=n,
∴,
∴BC=2a.
∵MN∥BE,MN⊥MC,
∴∠EFC=∠HMC=90°,
∴∠FCB+∠FBC=90°.
∵∠MBC=90°,
∴∠BMC+∠FCB=90°,
∴∠BMC=∠FBC.
∵∠MBC=∠BCE=90°,
∴△MBC∽△BCE,
∴=,
∴=,
∴n=4.
24.(12分)如图1,抛物线y=﹣x2+6x与x轴交于O、A两点,点P在抛物线上,过点P的直线y=x+m与抛物线的对称轴交于点Q.
(1)这条抛物线的对称轴是:直线 x=3 ,直线PQ与x轴所夹锐角的度数是 45 度;
(2)若S△POQ:S△PAQ=1:2,求此时的点P坐标;
(3)如图2,点M(1,5)在抛物线上,以点M为直角顶点作Rt△MEF,且E、F均在抛物线上,则所有满足条件的直线EF必然经过定点N,求点N坐标.
【解答】解:(1)抛物线y=﹣x2+6x的对称轴x=﹣=3,
∵直线PQ:y=x+m与直线y=x平行,
直线y=x是一、三象限的平分线,
∴直线PQ与x轴所夹锐角的度数是45°,
故答案为x=3,45.
(2)如图1中,作直线y=x交对称轴于H,连接AH,延长AH交直线PQ于M,作ON⊥PQ于N则四边形ONMH是矩形.△AOH是等腰直角三角形.
∵S△POQ:S△PAQ=1:2,
∴AM=2ON,
∴ON=MH=AH,
∵点A(6,0),H(3,3),
∴点M(0,6),
∴直线PQ的解析式为y=x+6,
由解得或,
∴点P坐标(2,4)或(3,3).
(3)如图2中,过点M作GH∥OA,过点E作EG⊥GH于G,过点F作FH⊥GH于H.
∵∠EMF=90°,
∴∠EMG+∠FMH=90°,
∵∠FMH+∠MFH=90°
∴∠EMG=∠MFH,∵∠G=∠H=90°,
∴△EMG∽△MFH,
∴=,设E(x1,y1)、F(x2,y2),直线EF的解析式为y=mx+n,
∴=,
∵y1=﹣x12+6x1,y2=﹣x22+6x2代入上式整理得到x1x2﹣5(x1+x2)+26=0
由消去y得到x2+(m﹣6)x+n=0,
∴x1+x2=6﹣m,x1x2=n,
∴n﹣5(6﹣m)+26=0,
∴n=4﹣5m,
∴直线EF解析式为y=mx+4﹣5m=(x﹣5)m+4,
当x=5时,y=4,
∴直线EF过定点N(5,4).
备注:以下内容仅显示部分,需完整版请下载!











