
高一理科
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,第Ⅰ卷为1-8题,共40分,第Ⅱ卷为9-20题,共110分.全卷共计150分.考试时间为120分钟.
第Ⅰ卷(本卷共40分)
一、选择题:(本大题共8题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.不等式的解集是( )
A. B. C. D.
2.已知等差数列中,的值是( )
A.15
B.30
C.31
D.64
3.过点(-1,3)且垂直于直线的直线方程为( )
A.
B.
C.
D.
4.已知等比数列的公比为正数,且·=2,=1,则=( )
A. B. C. D.2
5.在中,若,,,则=( )
A. B. C. D.
6.已知点(,)(N*)都在函数()的图象上,则与的大小关系是( )
A.> B.<
C.= D.与的大小与有关
7.如图,正方形的边长为,延长至,使,
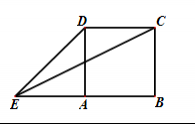
连接、,则( )
A. B. C. D.
8.已知整数按如下规律排成一列:、、、、,,,,,,……,则第70个数对是( )
A. B. C. D.
第Ⅱ卷(本卷共计110分)
二、填空题:(本大题共6小题,每小题5分,共30分)
9.已知两条直线若,则 .
10.若,则下列不等式①;②③;④中,正确的不等式是 .(填写正确序号)
11.已知点P在直线上,则的最小值为 .
12.在中,若,AB=5,BC=7,则的面积S=__________.
13.在中,角所对边长分别为,若,则的最小值为 .
14.等比数列的首项为,公比.设表示该数列的前n项的积,
则当n= 时,有最大值.
三、解答题:(本大题共6小题,共80分,解答应写出文字说明,证明过程,或演算步骤)
15.(本小题满分12分)
(Ⅰ)求以下不等式的解集:
(1) (2)
(Ⅱ)若关于x的不等式的解集为,求实数m的值.
16.(本小题满分12分)
已知三个顶点的直角坐标分别为A(3,4)、B(0,0)、C(c,0).
(Ⅰ)若,求c的值;
(Ⅱ)若c=5,求sin∠A的值.
17.(本小题满分14分)
等比数列的各项均为正数,且
(Ⅰ)求数列的通项公式;
(Ⅱ)设求数列的前n项和;
(III)设,求证:.
18.(本小题满分14分)
如图所示,某海岛上一观察哨A在上午11时测得一轮船在海岛北偏东的C处,12时20分测得船在海岛北偏西的B处,12时40分轮船到达位于海岛正西方且距海岛5km的E港口,如果轮船始终匀速直线前进,问船速多少?
19.(本小题满分14分)
已知点到直线l:的距离为.数列{an}的首项,且点列均在直线l上.
(Ⅰ)求b的值;
(Ⅱ)求数列{an}的通项公式;
(III)求数列的前n项和.
20.(本小题满分14分)
已知数列{an}的前n项和为,且满足,数列满足,为数列的前n项和.
(Ⅰ)求数列{an}的通项公式;
(Ⅱ)若对任意的,不等式恒成立,求实数的取值范围;
(III)是否存在正整数m,n(1<m<n),使得,,成等比数列?若存在,求出所有m,n的值;若不存在,请说明理由.
参考答案
一.选择题:(本大题共8题,每小题5分,共40分,在每小题给出的四个选项中,只有一项是符合题目要求的)
题号
1
2
3
4
5
6
7
8
答案
A
A
A
B
B
A
B
C
第Ⅱ卷(本卷共计110分)
二、填空题:(本大题共6小题,每小题5分,共30分)
9.2 10. ①④ 11. 12. 13. 14.
14.解
,
∵,
∴当n≤10时,>1,∴ | f(11) |>| f(10) |>…>| f(1) |;
当n≥11时,<1,∴ | f(11) |>| f(12) |>…
∵,∴的最大值为或中的最大者.
∵,
∴ 当n=12时,有最大值为.
三、解答题:(本大题共6小题,共80分,解答应写出文字说明,证明过程,或演算步骤)
15.(本小题12分)
(Ⅰ)求以下不等式的解集:
1. 2.
(Ⅱ)若关于x的不等式的解集为,求m的值.
解:(Ⅰ)1. 的解集为 3分
2. 的解集为 7分
(Ⅱ)若关于x的不等式的解集为,则0,2是的解.故
,解得,所以 12分
16.(本小题满分12分)
已知三个顶点的直角坐标分别为A(3,4)、B(0,0)、C(c,0).
(Ⅰ)若,求c的值;
(Ⅱ)若c=5,求sin∠A的值.
(1)
由 得 5分
(2)
12分
17.(本小题14分)
等比数列的各项均为正数,且
(Ⅰ)求数列的通项公式;
(Ⅱ)(Ⅱ)设求数列的前n项和.
(III)设,求证:.
解:(Ⅰ)设数列的公比为q,由得所以。
由条件可知a>0,故。 2分
由得,所以。 4分
故数列的通项式为an=。 5分
(Ⅱ)
9分
(III), 则
14分
18.(本小题满分14分)
如图所示,某海岛上一观察哨A上午11时测得一轮船在海岛北偏东的C处,12时20分测得船在海岛北偏西的B处,12时40分轮船到达位于海岛正西方且距海岛5km的E港口,如果轮船始终匀速直线前进,问船速多少?
解:轮船从C到B用时80分钟,从B到E用时20分钟,
而船始终匀速前进,由此可见:BC=4EB,设EB=,则
则BC=4,由已知得 2分
在△AEC中,由正弦定理得:
5分
在△ABC中,由正弦定理得:
8分
在△ABE中,由余弦定理得:
11分
所以船速 答:该船的速度为 km/h 14分
19.(本小题满分14分)
已知点到直线l:的距离为.数列{an}的首项,且点列均在直线l上.
(Ⅰ)求b的值;
(Ⅱ)求数列{an}的通项;
(III)求数列的前n项和.
解:(Ⅰ)由点到直线l:的距离为,得
,解得b=2 3分
(Ⅱ)数列{an}满足,即,故是以2为首项,公比为3的等比数列,故,即 8分
(III)数列的通项,故由分组求和,错位相减求和得
14分
20.(本小题满分14分)
已知数列{an}的前n项和为,且满足,数列满足,为数列的前n项和,
(Ⅰ)求数列{an}的通项和;
(Ⅱ)若对任意的,不等式恒成立,求实数的取值范围;
(III)是否存在正整数m,n(1<m<n),使得,,成等比数列?若存在,求出所有m,n的值;若不存在,请说明理由。
解:(1)由得, 3分
,
∴。 5分
(2)①当n为偶数时,要使不等式恒成立,
即需不等式恒成立,
,等号在n=2时取得
∴此时λ需满足λ<25; 7分
②当n为奇数时,要使不等式恒成立,即需不等式恒成立,
是随n的增大而增大,
∴n=1时,取得最小值-6
∴此时λ需满足λ<-21; 9分
综合①、②可得λ的取值范围是λ<-21。 10分
(3),
若成等比数列,
则,
由,
即,
∴, 12分
又m∈N,且m>1,
所以m=2,此时n=12,
因此,当且仅当m=2,n=12时,数列{Tn}中的成等比数列。 14分











