海淀区高二年级第二学期期中练习
数 学(文科)
学校 班级 姓名 成绩
本试卷共100分.考试时间90分钟.
一、选择题:本大题共8小题, 每小题4分,共32分. 在每小题给出的四个选项中,只有一项是符合题目要求的.
1.复数的虚部是( )
A. B. C. D.
2.下列导数运算错误的是( )
A. B. C. D.
3. 函数的图象如图所示,则的极大值点的个数为( )
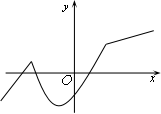
A. 0 B. 1
C. 2 D. 3
4.已知函数的导函数.若在上单调递增,则实数的取值范围是( )
A. B. C. D.
5. 已知两个命题:
“若复数满足,则.”
“存在唯一的一个实数对使得.”
其真假情况是( )
A.真假 B. 假假 C. 假真 D. 真真
6. 一个高为H容积为V的鱼缸的轴截面如图所示.现向空鱼缸内注水,直到注满为止.当鱼缸水深为h时,水的体积记为v.函数v=f(h)的大致图象可能是( )
7.已知函数在上可导,其部分图象如图所示,设,则下列不等式正确的是( )
8.已知函数,其导函数的图象如图所示,则函数的图象只可能是( )
二、填空题:本大题共4小题, 每小题4分,共16分.把答案填在题中横线上.
9.计算=_________.
10.已知 ,则______________.
11. 若函数是增函数,则实数的范围是_______________.
12. 已知数列满足,且,则________,通项______________(用表示).
三、解答题:本大题共5小题,共52分. 解答应写出文字说明,证明过程或演算步骤.
13.(本小题12分)
已知函数,其导函数为的部分值如下表所示:
|
|
-2 |
0 |
1 |
3 |
8 |
|
|
-10 |
6 |
8 |
0 |
-90 |
根据表中数据,回答下列问题:
(Ⅰ)实数的值为___________;当 ________时,取得极大值(将答案填写在横线上).
(Ⅱ)求实数,的值.
(Ⅲ)求的单调区间.
14.(本小题10分)
如图,四棱锥的底面满足 DE //AC,AC=2DE.
(Ⅰ)若DC⊥平面ABC, AB⊥BC,求证:平面ABE⊥平面BCD;
某同学用分析法证明第(1)问,用反证法证明第 (2)问,证明过程如下,请你在横线上填上合适的内容.
(Ⅰ)证明:欲证平面平面BCD,
只需证_______________________________,
由已知AB⊥BC,只需证________________,
由已知DC⊥平面ABC可得DC⊥AB成立,
所以平面ABE⊥平面BCD.
(Ⅱ)证明:假设______________________________________,
又因为平面,所以平面.
又因为平面平面=,
所以__________________,
又因为DE //AC,所以是平行四边形,
所以,这与_____________________________矛盾,
所以假设错误,原结论正确.
15.(本小题12分)
已知函数().
(Ⅰ)若直线是函数在点处的切线,求实数的值;
(Ⅱ)若对任意的,都有成立,求实数的取值范围.
16. (本小题10分)
请阅读问题1的解答过程,然后借鉴问题1的解题思路完成问题2的解答:
问题1:已知数集具有性质:
对任意的,与两数中至少有一个属于.若数集具有性质,求的值.
|
解:对于集合中最大的数,因为,,. 所以,,都属于该集合. 又因为,所以. 所以,,故. |
问题2:已知数集具有性质:
对任意的,与两数中至少有一个属于.若数集具有性质,求的值.
17. (本小题8分)
阅读下面的一段文字,并解决后面的问题:
我们可以从函数的角度来研究方程的解的个数的情况,例如,研究方程的解的情况:因为方程的同解方程有,等多种形式,所以,我们既可以选用函数,也可以选用函数,通过研究两函数图象的位置关系来研究方程的解的个数情况.因为函数的选择,往往决定了后续研究过程的难易程度,所以从函数的角度来研究方程的解的情况,首先要注意函数的选择.
请选择合适的函数来研究该方程的解的个数的情况,记为该方程的解的个数.请写出的所有可能取值,并对的每一个取值,分别指出你所选用的函数,画出相应图象(不需求出的数值).
参考答案
一、选择题:本大题共8小题, 每小题4分,共32分.
AABD CABD
二、填空题:本大题共4小题, 每小题4分,共16分.
9. 10. 11. 12. 9
(说明:一题两空的题目,每空2分)
三、解答题:本大题共5小题,共52分. 解答应写出文字说明,证明过程或演算步骤.
13.(本小题12分)
(Ⅰ)6,3. —————————————————————–4分
(Ⅱ)解:,————————————————————-5分
由已知表格可得解得——————————————–7分
(Ⅲ)解:由(Ⅱ)可得,———————8分
因为和时,时,——-10分
所以的单调增区间为,单调减区间为和.——–12分
14.(本小题10分)
(Ⅰ)证明:欲证平面平面BCD,
只需证平面, ————————————————————2分
由已知AB⊥BC,只需证,————————————————-4分
由已知DC⊥平面ABC可得DC⊥AB成立,
所以平面ABE⊥平面BCD.
(Ⅱ)证明:假设在平面内存在直线与平行,———————————6分
又因为平面,所以平面.
又因为平面平面=,
所以, —————————————8分
又因为DE //AC,所以是平行四边形,
所以,这与矛盾,———————————————10分
所以假设错误,原结论正确.
15.(本小题12分)
(Ⅰ)解:因为,.———————————————————-2分
由已知可得,解得.—————————————-3分
因为,所以,解得.——————————–4分
(Ⅱ)解1:当时,因为,所以不合题意.———————-6分
当时,对任意,都有成立.——–7分
当时,令,解得,
情况如下:
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
—————————————9分
所以的最大值为. ————————————————-10分
所以,依题意有,————————11分
因为,所以,即.
综上,所求的取值范围为.———————————————-12分
解2:对任意的,都有成立,即成立,
设,
当时,因为,显然不恒成立.—————6分
当时,不等式显然成立.—————————————————–7分
当时,,则,的情况如下:
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
——————————-9分
所以的最大值为,——————————————–10分
故只需,即.———————————————————11分
综上,所求的取值范围为.———————————————-12分
16. (本小题10分)
解:对于集合中最大的数,因为,,————2分
所以,,,都属于该集合.—————————————4分
又因为,所以.——————6分
所以,,————————————————————-8分
即.——————————————————————————-10分
17. (本小题8分)
解:的可能取值为0,1,2,3.
|
的可能取值 |
所选用的函数 |
图象位置关系 |
|
|
|
与 |
|
2分 |
|
|
与 |
|
2分
|
|
|
与 |
|
2分
|
|
|
与 |
|
2分 |
说明:其它选择函数的方法相对应给分即可。
备注:以下内容仅显示部分,需完整版请下载!











