2020届高考文科数学复习练习题(二):函数 专题训练
2020届高考文科数学复习练习题(二):函数 专题训练,高考文科数学复习,函数,莲山课件.
专题三 三角函数与解三角形
三角函数是一种重要的基本初等函数,它是描述周期现象的一个重要函数模型,可以加深对函数的概念和性质的理解和运用.其主要内容包括:三角函数的概念、三角变换、三角函数、解三角形等四部分.
在掌握同角三角函数的基本关系式、诱导公式、两角和与两角差、二倍角的正弦、余弦、正切公式的基础上,能进行简单三角函数式的化简、求值和恒等式证明;理解并能正确解决正弦函数、余弦函数、正切函数的图象和性质问题;运用三角公式和正弦定理、余弦定理解斜三角形.重点考查相关的数学思想方法,如方程的思想、数形结合、换元法等.
§3-1 三角函数的概念
【知识要点】
1.角扩充到任意角:通过旋转和弧度制使得三角函数成为以实数为自变量的函数.
2.弧度rad以及度与弧度的互化:.
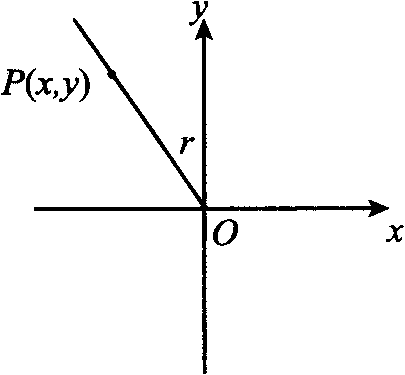
3.三角函数的定义:在平面直角坐标系中,任意角a 的顶点在原点,始边在x轴正半轴上,终边上任意一点P(x,y),|OP|=r(r≠0),则
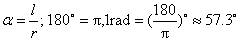
4.三角函数的定义域与值域:
|
函数 |
定义域 |
值域 |
|
y=sinx |
R |
[-1,1] |
|
y=cosx |
R |
[-1,1] |
|
y=tanx |
|
R |
5.三角函数线:正弦线,余弦线,正切线
6.同角三角函数基本关系式:
7.诱导公式:任意角a 的三角函数与角等的三角函数之间的关系,可以统一为“k·±a ”形式,记忆规律为“将a 看作锐角,符号看象限,(函数名)奇变偶不变”.
【复习要求】
1.会用弧度表示角的大小,能进行弧度制与角度制的互化;会表示终边相同的角;会象限角的表示方法.
2.根据三角函数定义,熟练掌握三角函数在各个象限中的符号,牢记特殊角的三角函数值,
3.会根据三角函数定义,求任意角的三个三角函数值.
4.理解并熟练掌握同角三角函数关系式和诱导公式.
【例题分析】
例1 (1)已知角a 的终边经过点A(-1,-2),求sina ,cosa ,tana 的值;
(2)设角a 的终边上一点,且,求y的值和tana .
解:(1),
所以
(2)
得,解得
【评析】利用三角函数的定义求某一角三角函数值应熟练掌握,同时应关注其中变量的符号.
例2 (1)判断下列各式的符号:
①sin330°cos(-260°)tan225° ②sin(-3)cos4
(2)已知cosq <0且tanq <0,那么角q 是( )
A.第一象限角 B.第二象限角 C.第三象限角 D.第四象限角
(3)已知a 是第二象限角,求角的终边所处的位置.
解:如图3-1-1,图3-1-2
(1)①330°是第四象限角,sin330°<0;-260°是第二象限角,cos(-260°)<0;225°是第三象限角,tan225°>0;所以sin330°cos(-260°)tan225°>0.
②-3是第三象限角,sin(-3)<0;5是第四象限角,cos5>0,所以sin(-3)cos5<0
或:-3≈-3×57.3°=-171.9°,为第三象限角;5≈5×57.3°=286.5°,是第四象限角
【评析】角的终边所处的象限可以通过在坐标系中逆时针、顺时针两个方向旋转进行判断,图3-1-1,图3-1-2两个坐标系应予以重视.
(2)cosq <0,所以角q 终边在第二或第三象限或在x轴负半轴上tanq <0,所以角q 终边在第二或第四象限中,所以角q 终边在第二象限中,选B.
【评析】角的终边在各个象限中时角的函数值的符号应熟练掌握,
(3)分析:容易误认为是第一象限角,其错误原因为认为第二象限角的范围是
a 是第二象限角,所以2kp+<a <2kp+p,(k∈Z),所以如下图3-1-3,可得是第一象限或第三象限角,又4kp+p<2a <4kp+2p,2a 是第三象限或第四象限角或终边落在y轴负半轴的角.
【评析】处理角的象限问题常用方法
(1)利用旋转成角,结合图3-1-1,图3-1-2,从角度制和弧度制两个角度处理;
(2)遇到弧度制问题也可以由°≈57.3°化为角度处理;
(3)在考虑角的终边位置时,应注意考虑终边在坐标轴上的情况.
(4)对于象限角和轴上角的表示方法应很熟练.
如第一象限角:,注意防止的错误写法.
例3 (1)已知tana =3,且a 为第三象限角,求sina ,cosa 的值;
(2)已知,求sina +tana 的值;
(3)已知tana =-2,求值:①;②sin2a +sina cosa .
解:(1)因为a 为第三象限角,所以sina <0,cosa <0
,得到
(2)因为,且不等于-1,所以a 为第二或第三象限角,
当a 为第二象限角时,sina >0,
所以
当a 为第三象限角时,sina <0,
所以
综上所述:当a 为第二象限角时,,当a 为第三象限角时,
【评析】已知一个角的某一个三角函数值,求其余的三角函数值的步骤:
(1)先定所给角的范围:根据所给角的函数值的符号进行判断
(2)利用同角三角函数的基本关系式,求其余的三角函数值(注意所求函数值的符号)
(3)当角的范围不确定时,应对角的范围进行分类讨论
(3)(法一):因为tana =-2,所以
①原式,
②原式=(-2cosa )2+(-2cosa )cosa =2cos2a ,
因为,得到,所以
(法二):①原式
②原式
【评析】已知一个角的正切值,求含正弦、余弦的齐次式的值:
(1)可以利用将切化弦,使得问题得以解决;
(2)1的灵活运用,也可以利用sin2a +cos2a =1,,将弦化为切.
例4 求值:
(1)tan2010°=______; (2)=______;
(3)
解:(1)tan2010°=tan(1800°+210°)=tan210°=tan(180°+30°)=
(2)
或:
【评析】“将a 看做锐角,符号看象限,(函数名)奇变偶不变”,,可以看出是的-2倍(偶数倍),借助图3-1-2看出为第二象限角,正弦值为正.
(3)原式
【分析】,将a 看做锐角,借助图3-1-2看出为第三象限角,正弦值为负,的3倍(奇数倍),改变函数名,变为余弦,所以可得,同理可得,所以原式.
【评析】诱导公式重在理解它的本质规律,对于“将a 看做锐角,符号看象限,(函数名)奇变偶不变”要灵活运用,否则容易陷入公式的包围,给诱导公式的应用带来麻烦.
例5 已知角a 的终边经过点,则a 的值为( )
A. B. C D.
解:因为,所以点在第二象限中,由三角函数定义得,
,因为角a 的终边在第二象限,
所以,
所以,,选D.
例6 化简下列各式:
(1)若q 为第四象限角,化简 (2)化简
(3)化简
解:(1)原式=,
因为q 为第四象限角,所以cosq >0,原式=,
(2)原式=
当q 为第二、三象限角或终边在x轴负半轴上时,cosq <0,所以原式,
当q 为第一、四象限角或终边在x轴正半轴上时,cosq >0,所以原式.
(3)原式.
4弧度属于第三象限角,所以sin4<0,cos4<0,
所以原式=-(sin4+cos4)=-sin4-cos4.
【评析】利用同角三角函数关系式化简的基本原则和方法:
(1)函数名称有弦有切:切化弦;(2)分式化简:分式化整式;
(3)根式化简:无理化有理(被开方式凑平方),运用,注意对符号的分析讨论;
(4)注意公式(sina ±cosa )2=1±2sina cosa =1±sin2a 的应用.
例7 扇形的周长为定值L,问它的圆心角q (0<q <p)取何值时,扇形的面积S最大?并求出最大值.
解:设扇形的半径为,则周长L=r·q +2r(0<q <p)
所以.
因为,当且仅当,即q =2∈(0,p)时等号成立.
此时,所以,当q =2时,S的最大值为.
练习3-1
一、选择题
1.已知,角a 终边上一点P(-2,t),则t的值为( )
A. B. C. D.
2.“tana =1”是“”的( )
A.充分而不必要条件 B.必要不而充分条件
C.充要条件 D.既不充分也不必要条件
3.已知点P(sina -cosa ,tana )在第一象限,则在[0,2p]上角a 的取值范围是( )
A. B.
C. D.
4.化简( )
A.sin10°+cos10° B.sin10°-cos10°
C.cos10°-sin10° D.-sin10°-cos10°
二、填空题
5.已知角a ,b 满足关系,则a -b 的取值范围是______.
6.扇形的周长为16,圆心角为2弧度,则扇形的面积为______.
7.若,则tan(p-a )=______.
8.已知:,则cosa -sina =______.
三、解答题
9.已知tana =-2,且cos(p+a )<0,求
(1)sina +cosa 的值 (2)的值
10.已知,求值:
(1); (2)cos2a -2sina cosa .
11.化简
§3-2 三角变换
【知识要点】
1.两角和与差的正弦、余弦、正切公式
sin(a +b )=sina cosb +cosa sinb ;sin(a -b )=sina cosb -cosa sinb ;
cos(a +b )=cosa cosb -sina sinb ;cos(a -b )=cosa cosb +sina sinb ;
2.正弦、余弦、正切的二倍角公式
sin2a =2sina cosa :
cos2a =cos2a -sin2a =1-2sin2a =2cos2a -1;
【复习要求】
1.牢记两角和、差、倍的正弦、余弦、正切公式,并熟练应用;
2.掌握三角变换的通法和一般规律;
3.熟练掌握三角函数求值问题.
【例题分析】
例1 (1)求值sin75°=______;
(2)设,则______;
(3)已知角的终边经过点(-1,-2),则的值为______;
(4)求值______.
解:(1)
.
(2)因为,
(3)由三角函数定义得,,
所以.
(4)
【评析】两角的和、差、二倍等基本三角公式应该熟练掌握,灵活运用,这是处理三角问题尤其是三角变换的基础和核心.注意和运用.
例2 求值:
(1)______;
(2)cos43°cos77°+sin43°cos167°=______;
(3)______.
解:(1)原式
.
【评析】辅助角公式:
应熟练掌握,另外本题还可变形为
(2)分析所给的角有如下关系:77°+43°=120°,167°=90°+77°,
原式=cos43°cos77°+sin43°cos(90°+77°)=cos43°cos77°-sin43°sin77°
=cos(43°+77°)=cos120°=
(3)分析所给的角有如下关系:37°+23°=60°,函数名均为正切,而且出现两角正切的和tana+tanb 与两角正切的积tana tanb ,所有均指向公式
∵
∴
∴.
【评析】三角变换的一般规律:看角的关系、看函数名称、看运算结构.以上题目是给角求值问题,应首看角的关系:先从所给角的关系入手,观察所给角的和、差、倍是否为特殊角,然后看包含的函数名称,以及所给三角式的结构,结合三角公式,找到题目的突破口.公式的变形tana +tanb =tan(a +b )(1-tana tanb )应予以灵活运用.
例3 ,则tan2a =______;
(2)已知,求的值.
解:(1)分析所给的两个已知角a +b ,a -b 和所求的角2a 之间有关系(a +b )+(a -b )=2a ,
,
(2)∵,∴,
又∵,∴;
∵,∴.
.
【评析】此类题目重在考察所给已知角与所求角之间的运算关系,主要是指看两角之间的和、差、倍的关系,如
等,找到它们的关系可以简化运算,同时在求三角函数值时应关注函数值的符号.
例4 如图,在平面直角坐标系xOy中,以Ox轴为始边做两个锐角a ,b ,它们的终边分别与单位圆相交于A,B两点,已知A,B的横坐标分别为.
(Ⅰ)求tan(a +b )的值;
(Ⅱ)求a +2b 的值.
解:由三角函数定义可得,
又因为a ,b 为锐角,所以,因此tana =7,
(Ⅰ);
(Ⅱ) ,所以,
∵a ,b 为锐角,∴
【评析】将三角函数的定义、两角和的正切、二倍角的正切公式结合在一起进行考查,要求基础知识掌握牢固,灵活运用;根据三角函数值求角,注意所求角的取值范围.
例5 化简(1);(2)
解:(1)原式
(2)法一:原式
法二:
原式
【评析】在进行三角变换时,应从三个角度:角的关系、函数的名称、所给运算式的结构全面入手,注意二倍角的变式(降幂升角)和辅助角公式的应用,此类变换是处理三角问题的基础.
例6 (1)已知a 为第二象限角,且,求的值.
(2)已知,求sin2x的值.
解:(1)因为a 为第二象限角,且,所以,
原式
【评析】此类题目为给值求值问题,从分析已知和所求的三角式关系入手,如角的关系,另一个特征是往往先对所求的三角式进行整理化简,可降低运算量.
(2)因为
所以
【评析】在进行三角变换时,应从三个角度:角的关系、函数的名称、所给运算式的结构全面入手,注意二倍角的变式(降幂升角)和辅助角公式的应用,此类变换是处理三角问题的基础,因为处理三角函数图象性质问题时往往先进行三角变换.
练习3-2
一、选择题
1.已知,则等于( )
A. B.7 C. D.-7
2.cos24°cos54°-sin24°cos144°=( )
A. B. C. D.
3.( )
A.sin15°-cos15° B.sin15°+cos15°
C.-sin15°-cos15° D.cos15°-sin15°
4.若,则cosa +sina 的值为( )
A. B. C. D.
二、填空题
5.若,则cos2q =______.
6.______.
7.若,则tana tanb =______.
8.已知,则______.
三、解答题
9.证明
10.已知a 为第四象限角,且,求的值.
11.已知a 为第三象限角,且.
(1)求sina +cosa 的值;
(2)求的值.
§3-3 三角函数
【知识要点】
1.函数y=sinx,y=cosx,y=tanx的图象性质.
|
性质 |
y=sinx |
y=cosx |
y=tanx |
|
|
一周期简图 |
|
|
|
|
|
最小正周期 |
2π |
2π |
π |
|
|
奇偶性 |
奇函数 |
偶函数 |
奇函数 |
|
|
单调性 |
增区间 |
|
[2kπ+π,2kπ+2π],k∈Z |
上是增函数 |
|
减区间 |
|
[2kπ,2kπ+π],k∈Z |
||
|
对称性 |
对称轴 |
|
x=kπ,k∈Z |
对称中心 |
|
对称 中心 |
(kπ,0),k∈Z |
|
||
2.三角函数图象是研究三角函数的有效工具,应熟练掌握三角函数的基本作图方法.会用“五点法”画正弦函数、余弦函数和函数y=Asin(w x+)(A>0,w >0)的简图.
3.三角函数是描述周期函数的重要函数模型,通过三角函数体会函数的周期性.函数y=Asin(w x+)(w ≠0)的最小正周期:;y=Atan(w x+)(w ≠0)的最小正周期:.同时应明确三角函数与周期函数是两个不同的概念,带三角函数符号的函数不一定是周期函数,周期函数不一定带三角函数符号.
【复习要求】
1.掌握三角函数y=sinx,y=cosx,y=tanx的图象性质:定义域、值域(最值)、单调性、周期性、奇偶性、对称性等.
2.会用五点法画出函数y=sinx,y=cosx,y=Asin(w x+)(A>0,w >0)的简图,掌握图象的变换方法,并能解决相关图象性质的问题.
3.本节内容应与三角恒等变换相结合,通过变换,整理出三角函数的解析式,注意使用换元法,转化为最基本的三个三角函数y=sinx,y=cosx,y=tanx,结合三角函数图象,综合考察三角函数性质
【例题分析】
例1 求下列函数的定义域
(1);(2).
解:(1)cosx≠0,定义域为
(2)sin2x≥0,由正弦函数y=sinx图象
(或利用在各象限中和轴上角的正弦函数值的符号可得终边在第一二象限,x轴,y轴正半轴上)
可得2kp≤2x≤2kp+p,
定义域为
例2 求下列函数的最小正周期
(1);(2);;
(4)y=2sin2x+2sinxcosx;(5)y=|sinx|.
解:(1).(2).
(3),所以.
(4),所以T=p.
(5)y=|sinx|的图象为下图,可得,T=p.
【评析】(1)求三角函数的周期时,通常利用二倍角公式(降幂升角)和辅助角公式先将函数解析式进行化简,然后用(正余弦)或(正切)求最小正周期.
(2)对于含绝对值的三角函数周期问题,可通过函数图象来解决周期问题.
例3 (1)已知函数f(x)=(1+cos2x)sin2x,x∈R,则f(x)是( )
A.最小正周期为p的奇函数 B.最小正周期为p的偶函数
C.最小正周期为的奇函数 D.最小正周期为的偶函数
(2)若函数f(x)=2sin(2x+)为R上的奇函数,则=______.
(3)函数的图象( )
解:(1)
周期为,偶函数,选D
(2)f(x)为奇函数,f(-x)=-f(x),所以2sin(-2x+)=-2sin(2x+)对x∈R恒成立,
即sincos2x-cossin2x=-sin2xcos-cos2xsin,
所以2sincos2x=0对x∈R恒成立,
即sin=0,所以=kp,k∈Z.
【评析】三角函数的奇偶性问题可以通过奇偶性定义以及与诱导公式结合加以解决.如在本题(2)中除了使用奇偶性的定义之外,还可以从公式sin(x+p)=-sinx,sin(x+2p)=sinx得到当=2kp+p或=2kp+p,k∈Z,即=kp,k∈Z时,f(x)=2sin(2x+)可以化为f(x)=sinx或f(x)=-sinx,f(x)为奇函数.
2020届高考文科数学复习练习题(一):集合与常用逻辑用语 专题训练
2020届高考文科数学复习练习题(一):集合与常用逻辑用语 专题训练,高考文科数学复习,集合与常用逻辑用语,莲山课件.
(3)分析:首先考虑奇偶性,f(-x)=lncos(-x)=lncosx=f(x),为偶函数,排除掉B,D选项
考虑(0,)上的函数值,因为0<cosx<1,所以lncosx<0,应选A
【评析】处理函数图象,多从函数的定义域,值域,奇偶性,单调性等方面综合考虑.
例4 求下列函数的单调增区间
(1);(2) ;
(3) ;(4)
解:(1)y=cosx的增区间为[2kp+p,2kp+2p],k∈Z,
由可得
的增区间为,
(2)先求出函数的增区间
然后与区间[-p,0]取交集得到该函数的增区间为和,
(3),转化为问题(1),增区间为
(4)原函数变为,需求函数的减区间,
,得,
的增区间为
【评析】处理形如y=Asin(w x+)+k,(w <0)的函数单调性时,可以利用诱导公式将x的分数化正,然后再求相应的单调区间.
求三角函数单调区间的一般方法:
(1)利用三角变换将解析式化为只含有一个函数的解析式,利用换元法转化到基本三角函数的单调性问题.
(2)对于给定区间上的单调性问题,可采用问题(2)中的方法,求出所有的单调增区间,然后与给定的区间取交集即可.
例5 求下列函数的值域
(1)函数的最大值以及此时x的取值集合
(2)
(3)
(4)y=cos2x-2sinx
解:(1)当时,,函数的最大值为3,
此时x的取值集合为
(2)结合正弦函数图象得:当时,
该函数的值域为(-1,2]
(3)分析:利用换元法,转化为题(2)的形式.
,
设,则原函数变为,
结合余弦函数图象得:,所以函数的值域为(-1,2].
(4)y=-2sin2x-2sinx+1,
设t=sinx,则函数变为y=-2t2-2t+1,t∈[-1,1],
因为
结合二次函数图象得,当t=1时,函数最小值为-3,当时,函数最大值为,所以函数的值域为
【评析】处理三角函数值域(最值)的常用方法:
(1)转化为只含有一个三角函数名的形式,如y=Asin(w x+)+k,y=Acos(w x+)+k,y=Atan(w x+)+k等,利用换元法,结合三角函数图象进行处理.
(2)转化为二次型:如Asin2x+Bsinx+C,Acos2x+Bcosx+C形式,结合一元二次函数的图象性质求值域.
例6 函数y=sin(w x+)的图象(部分)如图所示,则w 和的取值是( )
A. B.
C. D.
解:,即,所以,
当时,,所以,选C
例7 (1)将函数的图象如何变换可得到函数的图象
(2)已知函数y=sinx的图象,将它怎样变换,可得到函数的图象
解:(1)
(2)法一:y=sinx
法二:y=sinx
【评析】由y=sinx的图象变换为y=Acos(w x+)(w >0)的图象时,特别要注意伸缩变换和横向平移的先后顺序不同,其横向平移过程中左右平移的距离不同.
例8 (1)函数的一条对称轴方程为( )
A. B. C. D.
(2)函数的对称轴方程和对称中心的坐标
解:(1)法一:的对称轴为,
即,当k=-1时,,选C
法二:将四个选项依次代入中,寻找使得函数取得最小值或最大值的选项
当时,,选C
(2) 的对称轴为,即
对称中心:此时
所以对称中心的坐标为
【评析】正余弦函数的对称轴经过它的函数图象的最高点或最低点,对称中心是正余弦函数图象与x轴的交点,处理选择题时可以灵活运用.
例9 已知函数的最小正周期为p.
(1)求w 的值.
(2)求f(x)在区间上的值域.
(3)画出函数y=2f(x)-1在一个周期[0,p]上的简图.
(4)若直线y=a与(3)中图象有2个不同的交点,求实数a的取值范围.
解:(1)
因为函数f(x)的最小正周期为p,且w >0,所以,解得w =1
(2)由(1)得,因为,所以,
结合正弦函数图象,得
因此,即f(x)的取值范围为
(3)由(1)得
列表
|
|
|
0 |
|
π |
|
|
|
x |
0 |
|
|
|
|
π |
|
y |
-1 |
0 |
2 |
0 |
-2 |
-1 |
(4)由图象可得,-2<a<2且a≠-1.
【评析】本节内容应与三角恒等变换相结合,利用降幂升角公式和辅助角公式等三角公式化简三角函数解析式,整理、变形为只含有一个函数名的解析式,如y=Asin(w x+)(w >0)或y=Acos(w x+)(w >0)的形式,利用换元法,结合y=sinx、y=cosx的图象,再研究它的各种性质,如求函数的周期,单调性,值域等问题,这是处理三角函数问题的基本方法.
练习3-3
一、选择题
1.设函数x∈R,则f(x)是( )
A.最小正周期为p的奇函数 B.最小正周期为p的偶函数
C.最小正周期为的奇函数 D.最小正周期为的偶函数
2.把函数y=sinx(x∈R)的图象上所有的点向左平行移动个单位长度,再把所得图象上所有点的横坐标缩短到原来的倍(纵坐标不变),得到的图象所表示的函数是( )
A. B.
C. D.
3.函数的图象( )
A.关于点(,0)对称 B.关于直线对称
C.关于点(,0)对称 D.关于直线对称
4.函数y=tanx+sinx-|tanx-sinx|在区间内的图象大致是( )
二、填空题
5.函数的最大值是______.
6.函数的最小正周期为______.
7.函数的图象的一部分如图所示,则该函数的解析式为y=______.
8.函数y=cos2x+cosx的值域为______.
三、解答题
9.已知函数f(x)=2cosx(sinx-cosx)+1,x∈R.
(Ⅰ)求函数f(x)的对称轴的方程;
(Ⅱ)求函数f(x)的单调减区间.
10.已知函数
(Ⅰ)求函数f(x)的最小正周期及最值;
(Ⅱ)令,判断函数g(x)的奇偶性,并说明理由.
11.已知,a为常数),且满足条件f(x1)=f(x2)=0的|x1-x2|的最小值为.
(Ⅰ)求w 的值;
(Ⅱ)若f(x)在上的最大值与最小值之和为3,求a的值.
§3-4 解三角形
【知识要点】
1.三角形内角和为A+B+C=p
,,注意与诱导公式相结合的问题.
2.正弦定理和余弦定理
正弦定理:,(r为△ABC外接圆的半径).
余弦定理:.
a2=b2+c2-2bccosA;b2=a2+c2-2accosB;c2=a2+b2-2abcosC.
3.在解三角形中注意三角形面积公式的运用:
×底×高.
absin
4.解三角形中注意进行“边角转化”,往往结合三角变换处理问题.
【复习要求】
1.会正确运用正余弦定理进行边角的相互转化;
2.会熟练运用正弦定理和余弦定理解决三角形中的求角,求边,求面积问题.
【例题分析】
例1 (1)在△ABC中,,b=1,B=30°,则角A等于( )
A.60° B.30° C.120° D.60°或120°
(2)△ABC中,内角A,B,C所对的边分别为a、b、c,满足等式(a+b)2=ab+c2,则角C的大小为______.
(3)在△ABC中,若sinA∶sinB∶sinC=5∶7∶8,则∠B的大小是______.
(4)在△ABC中,若,C=150°,BC=1,则AB=______.
解:(1)∵
又∵a>b,∴A>B=30°,∴A=60°或120°,
(2)∵(a+b)2=ab+c2,∴a2+b2-c2=-ab,
∴
(3)∵,sinA∶sinB∶sinC=5∶7∶8.
∴a∶b∶c=5∶7∶8,∴,∴B=60°.
(4)分析:已知条件为两角和一条对边,求另一条对边,考虑使用正弦定理,借助于求sinA
.
【评析】对于正弦定理和余弦定理应熟练掌握,应清楚它们各自的使用条件,做到合理地选择定理解决问题.
例2 (1)在△ABC中,acosA=bcosB,则△ABC一定是( )
A.直角三角形 B.等边三角形
C.等腰三角形 D.等腰三角形或直角三角形
(2)在△ABC中,2sinB·sinC=1+cosA,则△ABC的形状为( )
A.直角三角形 B.等边三角形
C.等腰三角形 D.等腰直角三角形
解:(1)法一:,acosA=bcosB,
∴sinAcosA=sinBcosB,∴sin2A=sin2B,
∵2A,2B∈(0,2p),∴2A=2B或2A+2B=p,
∴A=B或,选D.
法二:∵acosA=bcosB,
∴,
整理得(a2-b2)(a2+b2-c2)=0.
所以:a=b或a2+b2=c2,选D.
(2)∵2sinB·sinC=1+cosA,cos(B+C)=cos(p-A)=-cosA,
∴2sinB·sinC=1-(cosBcosC-sinBsinC),
∴cosBcosC+sinB·sinC=1,
∴cos(B-C)=1,
∵B,C∈(0,p),∴B-C∈(-p,p),
∴B-C=0,∴B=C,选C.
【评析】判断三角形形状,可以从两个角度考虑
(1)多通过正弦定理将边的关系转化为角的关系,进而判断三角形形状,
(2)多通过余弦定理将角的关系转化为边的关系,进而判断三角形形状,通常情况下,以将边的关系转化为角的关系为主要方向,特别需要关注三角形内角和结合诱导公式带给我们的角的之间的转化.
例3 已知△ABC的周长为,且sinA+sinB=sinC
(1)求边AB的长;
(2)若△ABC的面积为,求角C的度数.
解:(1)由题意及正弦定理,得
,解得AB=1.
(2)由△ABC的面积,得,
因为,所以(BC+AC)2=BC2+AC2+2AC·BC=2,
可得,由余弦定理,得,
所以C=60°.
例4 在△ABC中,∠A、∠B、∠C所对的边长分别为a、b、c,设a、b、c满足条件b2+c2-bc=a2和=,求∠A和tanB的值.
解(1)由已知和余弦定理得,所以∠A=60°.
(2)分析:所给的条件是边的关系,所求的问题为角,可考虑将利用正弦定理将边的关系转化为角的关系.
在△ABC中,sinC=sin(A+B)=sin(60°+B),
因为
所以
【评析】体现了将已知条件(边)向所求问题(角tanB→sina,cosa )转化,充分利用了正弦定理和三角形内角关系实现转化过程.
例5 在△ABC中,内角A,B,C对边的边长分别是a,b,c,已知c=2,.
(Ⅰ)若△ABC的面积等于,求a,b;
(Ⅱ)若sinC+sin(B-A)=2sin2A,求△ABC的面积.
解:(Ⅰ)由余弦定理及已知条件得,a2+b2-ab=4,
又因为△ABC的面积等于,所以,得ab=4.
联立方程组解得a=2,b=2.
(Ⅱ)由题意得sin(B+A)+sin(B-A)=4sinAcosA,
(sinBcosA+cosBsinA)+(sinBcosA-cosBsinA)=4sinAcosA,
即sinBcosA=2sinAcosA,
当cosA=0时,,
当cosA≠0时,得sinB=2sinA,由正弦定理得b=2a,
联立方程组解得.
所以△ABC的面积.
【评析】以上两例题主要考查利用正弦定理、余弦定理来确定三角形边、角关系等基础知识和基本运算能力.以及三角形面积公式的运用.同时应注意从题目中提炼未知与已知的关系,合理选择定理公式,综合运用正弦定理和余弦定理实现边角之间的转化.
例6 如图,测量河对岸的塔高AB时,可以选与塔底B在同一水平面内的两个测点C与D,现测得∠BCD=a ,∠BDC=b ,CD=s,并在点C测得塔顶A的仰角为q ,求塔高AB.
解:在△BCD中,∠CBD=p-a -b .
由正弦定理得
所以.
在Rt△ABC中,
例7 已知在△ABC中,sinA(sinB+cosB)-sinC=0,sinB+cos2C=0,求角A,B,C的大小.
解:sinAsinB+sinAcosB-sin(A+B)=0,
sinAsinB+sinAcosB-(sinAcosB+cosAsinB)=0,
sinAsinB-cosAsinB=sinB(sinA-cosA)=0,
因为sinB≠0,所以sinA-cosA=0,
所以tanA=1,,可得,
所以,
sinB+2sinBcosB=0,因为sinB≠0,所以.
【评析】考查了三角形中角的相互转化关系,同时兼顾了两角和、二倍角、诱导公式等综合应用.
练习3-4
一、选择题
1.在△ABC中,若A∶B∶C=1∶2∶3,则a∶b∶c=( )
A.1∶2∶3 B. C.1∶4∶9 D.
2.在△ABC中,角A、B、C的对边分别为a,b,c,,b=1,则c=( )
A.1 B.2 C. D.
3.△ABC中,若a=2bcosC,则△ABC的形状一定为( )
A.等边三角形 B.直角三角形 C.等腰三角形 D.等腰直角三角形
4.△ABC的三内角A,B,C的对边边长分别为a,b,c,若,A=2B,则cosB=( )
A. B. C. D.
二、填空题
5.在△ABC中,角A,B,C所对的边分别为a,b,c,若a=1,,则A=______.
6.在△ABC中,角ABC的对边分别为a、b、c,若,则角B的值为______.
7.设△ABC的内角,则2sinBcosC-sin(B-C)的值为______.
8.在三角形ABC中,∠A、∠B、∠C的对边分别为a、b、c,若bcosC=(2a-c)cosB,则∠B的大小为______.
三、解答题
9.在△ABC中,.
(Ⅰ)求角C的大小;
(Ⅱ)若AB的边长为,求边BC的边长.
10.如图,某住宅小区的平面图呈扇形AOC.小区的两个出入口设置在点A及点C处,小区里有两条笔直的小路AD,DC,且拐弯处的转角为120°.已知某人从C沿CD走到D用了10分钟,从D沿DA走到A用了6分钟.若此人步行的速度为每分钟50米.
求该扇形的半径OA的长(精确到1米).
11.在三角形ABC中,,求三角形ABC的面积S.
专题03 三角函数与解三角形参考答案
练习3-1
一、选择题:
1.B 2.B 3.B 4.C
二、填空题
5. 6.16 7. 8.
三、解答题
9.解:(1)
(2)原式=
10.解:(1)原式(2)原式
11.解:当k为偶数时,原式
当k为奇数时,原式,综上所述,原式=0.
练习3-2
一、选择题
1.A 2.C 3.D 4.C
二、填空题
5 6.4 7. 8.
三、解答题
9.解:左边右边.
10.解:原式,
因为a 为第四象限角,且,所以,
所以原式.
11.解:(1)由=可得,
所以=,
因为a 为第三象限角,所以sina <0,cosa <0,sina +cosa <0,
所以.
(2)原式
,
因为,所以,
所以原式
练习3-3
一、选择题
1.B 2.C 3.A 4.D
二、填空题
5.2 6.2 7. 8.
三、解答题
9.解:=.
(1),对称轴方程为,
(2),即,
f(x)的单调减区间为.
10.解:(I)∵
∴f(x)的最小正周期
当时,f(x)取得最小值-2;当时,f(x)取得最大值2.
(Ⅱ)由(I)知
∴函数g(x)是偶函数.
11.解:(1)
由满足条件f(x1)=f(x2)=0的|x1-x2|的最小值为,可得的最小正周期为p,所以w =1.
(2)
f(x)在上的最大值为a+3,最小值为a,
由题意得2a+3=3,所以a=0.
练习3-4
一、选择题
1.B 2.B 3.C 4.B
二、填空题
5. 6.或 7. 8.
三、解答题
9.解:(I)∵C=p-(A+B),∴tanC=-tan(A+B)=
又∵0<C<p,
(Ⅱ)由且,得
由得:所以
10.解:设该扇形的半径为r米.由题意,得CD=500(米),DA=300(米),∠CDO=60°在△CDO中,CD2+OD2-2·CD·OD·cos60°=OC2,
即5002+(r-300)2-2×500×(r-300)×=r2,
解得(米).
11.解:由题意,得,B为锐角,,
=,
已知,由正弦定理,得,
∴.
备注:以上内容仅显示部分,需完整版请下载!
2020届高考地理复习练习题(十三):环境环保 专题训练
2020届高考地理复习练习题(十三):环境环保 专题训练,高考地理复习,环境环保,莲山课件.











