专题1 二次函数
题型一 二次函数的图象和性质
例 1 对于抛物线y =-x 2+2x +3,有下列四个结论:①它的对称轴为x =1;
②它的顶点坐标为(1,4);
③它与y 轴的交点坐标为(0,3),与x 轴的交点坐标为(-1,0)和(3,0);
④当x >0时,y 随x 的增大而减小.
其中正确的个数为( C )
A .1
B .2
C .3
D .4
【解析】 ①对称轴为
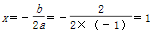
,∴①正确;②y =-x
2
+2x +3=-(x -1)
2
+4,∴它的顶点坐标为(1,4),∴②正确;③y =-x
2
+2x +3,当x =0时,y =3,当y =0时,-x
2
+2x +3=0,x 1=-1,x
2
=3,∴y =-x
2
+2x +3与y 轴的交点坐标为(0,3),与x 轴的交点坐标为(-1,0)和(3,0),∴③正确;④∵a =-1<0,∴当x >1时,y 随x 的增大而减小,∴④错误.故正确的选项有①②③三个.
【点悟】 二次函数的性质,常常从对称轴、顶点坐标、最大值(最小值),增减性等角度分析.
变式跟进
1.小张同学说出了二次函数的两个条件:
(1)当x <1时,y 随x 的增大而增大;
(2)函数图象经过点(-2,4).
则符合条件的二次函数表达式可以是( D )
A .y =-(x -1)2-5
B .y =2(x -1)2-14
C .y =-(x +1)2+5
D .y =-(x -2)2+20
2.求下列函数的图象的对称轴、顶点坐标及与x 轴的交点坐标.
(1)y =4x 2+24x +35;
(2)y =-3x 2+6x +2;
(3)y =x 2-x +3;
(4)y =2x 2+12x +18.
解:(1)∵y =4x 2+24x +35,
∴对称轴是直线x =-3,顶点坐标是(-3,-1),
解方程4x 2+24x +35=0,得x 1=-52,x 2=-72, 故它与x 轴交点坐标是
(2)∵y =-3x 2+6x +2,
∴对称轴是直线x =1,顶点坐标是(1,5),
解方程-3x 2+6x +2=0,
解方程x 2-x +3=0,无解,故它与x 轴没有交点;
(4)∵y =2x 2+12x +18,
∴对称轴是直线x =-3,顶点坐标是(-3,0),
当y =0时,2x 2+12x +18=0,∴x 1=x 2=-3,
∴它与x 轴的交点坐标是(-3,0).
题型二 二次函数的平移
例 2 将抛物线y =-2x 2+1向右平移1个单位长度,再向上平移1个单位长度所得的抛物线表达式为( C )
A .y =-2(x +1)2
B .y =-2(x +1)2+2
C .y =-2(x -1)2+2
D .y =-2(x -1)2+1
【点悟】
二次函数图象的平移实质上是顶点位置的变化,只要确定平移前、后的顶点坐标,就可以确定抛物线的平移规律.
变式跟进
3.将抛物线y =2x 2+4x -5的图象向左平移2个单位,再向上平移1个单位,所得抛物线表达式是( C )
A .y =2(x +1)2-7
B .y =2(x +1)2-6
C .y =2(x +3)2-6
D .y =2(x -1)2-6
题型三 二次函数与一元二次方程和不等式的关系
例 3 [2016·宁夏]若二次函数y =x 2-2x +m 的图象与x 轴有两个交点,则m 的取值范围是__m <1__.
【解析】 ∵二次函数y =x 2-2x +m 的图象与x 轴有两个交点,∴Δ>0,∴4-4m >0,∴m <1.
【点悟】 抛物线y =ax 2+bx +c (a ≠0)与x 轴的交点的横坐标x 1,x 2,就是方程ax 2+bx +c =0(a ≠0)的两个根,判断抛物线与x 轴是否有交点,只要判断b 2-4ac 与0的大小即可.
变式跟进
4.已知二次函数y =x 2-2x +m (m 为常数)的图象与x 轴的一个交点为(-1,0),则关于x 的一元二次方程x 2-2x +m =0的两个实数根是( D )
A .x 1=1,x 2=2
B .x 1=1,x 2=3
C .x 1=-1,x 2=2
D .x 1=-1,x 2=3
【解析】 二次函数y =x 2-2x +m (m 为常数)的对称轴是x =1,(-1,0)关于x =1的对称点是(3,0).则一元二次方程x 2-2x +m =0的两个实数根是x 1=-1,x 2=3.
5.[2017·高邮二模]如图1,二次函数y 1=ax 2+bx +c 与一次函数y 2=kx 的图象交于点A 和原点O ,点A 的横坐标为-4,点A 和点B 关于抛物线的对称轴对称,点B 的横坐标为1,则满足0<y 1<y 2的x 的取值范围是__-4<x <-3__.
图1 第5题答图
【解析】 如答图所示,∵点A 的横坐标为-4,点A 和点B 关于抛物线的对称轴对称,点B 的横坐标为1,∴抛物线的对称轴为x =,
∵二次函数y 1=ax 2+bx +c 与一次函数y 2=kx 的图象交于点A 和原点O ,∴C 点坐标为(-3,0),则满足0<y 1<y 2的x 的取值范围是-4<x <-3.
题型四 二次函数的图象与系数之间的关系
例 4 如图2,已知二次函数y =ax 2+bx +c (a ≠0)的图象与x 轴交于点A (-1,0),与y 轴的交点B 在(0,-2)和(0,-1)之间(不包括这两点),对称轴为直线x =1.下列结论:
①abc >0; ②4a +2b +c >0;
③4ac -b 2<8a ; ④13<a <23; ⑤b >c .
其中含所有正确结论的选项是( D)
图2
A .①③
B .①③④
C .②④⑤
D .①③④⑤
【解析】 ①∵函数开口方向向上,∴a >0,∵对称轴在原点右侧,∴ab 异号,∵抛物线与y 轴交点在y 轴负半轴,∴c <0,∴abc >0,故①正确;
②∵图象与x 轴交于点A (-1,0),对称轴为直线x =1,∴图象与x 轴的另一个交点为(3,0),
∴当x =2时,y <0,∴4a +2b +c <0,故②错误;
③∵图象与x 轴交于点A (-1,0),∴当x =-1时,y =(-1)2a +b ×(-1)+c =0,∴a -b +c =0,即a =b -c ,c =b -a ,∵对称轴为直线x =1,∴,即b =-2a ,∴c =b -a =(-2a )-a =-3a ,∴4ac -b 2=4a (-3a )-(-2a )2=-16a 2<0.∵8a >0,∴4ac -b 2<8a ,故③正确;
④∵图象与y 轴的交点B 在(0,-2)和(0,-1)之间,∴-2<c <-1,∴-2<-3a <-1,∴,故④正确;
⑤∵a >0,∴b -c >0,即b >c ,故⑤正确.
【点悟】 二次函数y =ax 2+bx +c (a ≠0),①二次项系数a 决定抛物线的开口方向和大小.当a >0时,抛物线向上开口;当a <0时,抛物线向下开口;|a |还可以决定开口大小,|a |越大开口就越小.②一次项系数b 和二次项系数a 共同决定对称轴的位置.当a 与b 同号时(即ab >0),对称轴在y 轴左侧;当a 与b 异号时(即ab <0),对称轴在y 轴右侧(简称:左同右异).③常数项c 决定抛物线与y 轴交点,抛物线与y 轴交于(0,c ).
变式跟进
6.[2016·孝感]如图3是抛物线y =ax 2+bx +c (a ≠0)的部分图象,其顶点坐标为(1,n ),且与x 轴的一个交点在点(3,0)和(4,0)之间.则下列结论:
①a -b +c >0; ②3a +b =0; ③b 2=4a (c -n );
④一元二次方程ax 2+bx +c =n -1有两个不相等的实数根.
其中正确结论的个数是( C)
图3
A .1
B .2
C .3
D .4
【解析】 ∵抛物线与x 轴的一个交点在点(3,0)和(4,0)之间,而抛物线的对称轴为直线x =1,∴抛物线与x 轴的另一个交点在点(-2,0)和(-1,0)之间.
∴当x =-1时,y >0,即a -b +c >0,∴①正确;
∵抛物线的对称轴为直线,即b =-2a ,∴3a +b =3a -2a =a ,∴②错误;
∵抛物线的顶点坐标为(1,n ),∴ ,∴b 2=4ac -4an =4a (c -n ),∴③正确; ∵抛物线与直线y =n 有一个公共点,∴抛物线与直线y =n -1有2个公共点,∴一元二次方程ax 2+bx +c =n -1有两个不相等的实数根,∴④正确.
题型五 二次函数的实际应用
例 5 [2016·潍坊]旅游公司在景区内配置了50辆观光车供游客租赁使用,假定每辆观光车一天内最多只能出租一次,且每辆车的日租金x (元)是5的倍数,发现每天的运营规律如下:当x 不超过100元时,观光车能全部租出;当x 超过100元时,每辆车的日租金每增加5元,租出去的观光车就会减少1辆,已知所有观光车每天的管理费是1 100元.
(1)优惠活动期间,为使观光车全部租出且每天的净收入为正,则每辆车的日租金至少应为多少元?(注:净收入=租车收入-管理费)
(2)当每辆车的日租金为多少时,每天的净收入最多?
解:(1)由题意知,若观光车能全部租出,则0≤x ≤100,由50x -1 100>0,解得x >22,
∵x 是5的倍数,∴每辆车的日租金至少为25元;
(2)设每天的净收入为y 元,当0≤x ≤100时,y 1=50x -1 100,∵y 1随x 的增大而增大,∴当x =100时,y 1的最大值为50×100-1 100=3 900.
当x >100时,
100=-15x 2+70x -1 100=-15(x -175)2+5 025. 当x =175时,y 2的最大值是5 025,∵5 025>3 900,
∴当每辆车的日租金为175元时,每天的净收入最多,最多收入是5 025元.
【点悟】 应用二次函数解决实际问题中的最优化问题,实际上就是求函数的最大值(或最小值).解题时,要先根据题目提供的条件确定函数关系式,并将它配成顶点式,y =a (x -h )2+k ,再根据二次函数的性质确定最大值或最小值.
变式跟进
7.[2016·杭州]把一个足球垂直水平地面向上踢,时间t (s)与该足球距离地面的高度h (m)适用公式h =20t -5t 2(0≤t ≤4).
(1)当t =3时,求足球距离地面的高度;
(2)当足球距离地面的高度为10 m 时,求t 的值;
(3)若存在实数t 1,t 2(t 1≠t 2),当t =t 1或t 2时,足球距离地面的高度都为m (m),求m 的取值范围. 解:(1)当t =3时,h =20t -5t 2=15(m),
∴此时足球离地面的高度为15 m ;
(2)∵h =10,∴20t -5t 2=10,
(3)∵m ≥0,由题意得t 1和t 2是方程20t -5t 2=m 的两个不相等的实数根,
∴b 2-4ac =202-20m >0,解得m <20,
∴m 的取值范围是0≤m <20.
题型六 二次函数的综合题
例 6 [2017·浙江月考]如图4,抛物线的顶点为A ,与x 轴的正半轴交于点B .
(1)将抛物线C 1上的点的横坐标和纵坐标都扩大到原来的2倍,求变换后得到的抛物线的表达式;
(2)将抛物线C 1上的点(x ,y )变为(kx ,ky )(|k |>1),变换后得到的抛物线记作C 2,抛物线C 2的顶点为C ,求抛物线C 2的表达式(用k 表示);
(3)在(2)条件下,点P 在抛物线C 2上,满足S △PAC =S △ABC ,且∠ACP =90°.当k >1时,求k 的值.
图4 例6答图
解:
∴抛物线C 1经过原点O ,点A (1, )和点B (2,0)三点,
2. 变式跟进
8.[2017·诸城校级月考]如图5,在矩形OABC 中,OA =5,AB =4,点D 为边AB 上一点,将△BCD 沿直线CD 折叠,使点B 恰好落在OA 边上的点E 处,分别以OC ,OA 所在的直线为x 轴,
y 轴建立平面直角坐标系.
图5
(1)求OE 的长;
(3)一动点P 从点C 出发,沿CB 以每秒2 个单位长的速度向点B 运动,同时动点Q 从E 点出发,沿EC 以每秒1个单位长的速度向点C 运动,当点P 到达点B 时,两点同时停止运动.设运动时间为t s ,当t 为何值时,DP =DQ .
1.已知,二次函数y =ax 2+bx +c (a ≠0)的图象如图1所示,则以下说法不正确的是(C)
图1
A .根据图象可得该函数y 有最小值
B .当x =-2时,函数y 的值小于0
C .根据图象可得a >0,b <0
D .当x <-1时,函数值y 随着x 的增大而减小
【解析】 由图象可知:A.抛物线开口向上,该函数y 有最小值,此选项正确;B.当x =-2时,图象在x 轴的下方,函数值小于0,此选项正确;C.对称轴为x =-1,a >0,则b >0,此选项错误;D.当x <-1时,y 随x 的增大而减小,此选项正确.
2.抛物线y =(x +2)2-1可以由抛物线y =x 2
平移得到,下列平移方法中正确的是( B )
A .先向左平移2个单位,再向上平移1个单位
B .先向左平移2个单位,再向下平移1个单位
C .先向右平移2个单位,再向上平移1个单位
D .先向右平移2个单位,再向下平移1个单位
【解析】 ∵函数y =x 2的图象沿x 轴向左平移2个单位长度,得y =(x +2)2;然后y 轴向下平移1个单位长度,得y =(x +2)2-1,故选B.
3.一次函数y =ax +b (a ≠0)与二次函数y =ax 2+bx +c (a ≠0)在同一平面直角坐标系中的图象可能是( C
A B C D
4.如图2,二次函数y =ax 2+bx +c (a ≠0)的图象与x 轴交于点A (-1,0),其对称轴为直线x =1,下列结论中正确的是( D)
图2
A .abc >0
B .2a -b =0
C .4a +2b +c <0
D .9a +3b +c =0
【解析】 ∵抛物线的开口向下,则a <0,对称轴在y 轴的右侧,∴b >0,图象与y 轴交于正半轴上,∴c >0,∴abc <0;∵对称轴为x =1,∴,∴-b =2a ,∴2a +b =0;当x =2时,4a +2b +c >0;当x =3时,9a +3b +c =0.
5.已知二次函数y =3x 2+36x +81.
(1)写出它的顶点坐标;
(2)当x 取何值时,y 随x 的增大而增大;
(3)求出图象与x 轴的交点坐标;
(4)当x 取何值时,y 有最小值,并求出最小值;
(5)当x 取何值时,y <0.
解:(1)∵y =3x 2+36x +81=3(x +6)2-27,
∴顶点坐标为(-6,-27);
(2)∵抛物线的对称轴为x =-6,且抛物线的开口向上,
∴当x >-6时,y 随x 的增大而增大;
(3)当3x 2
+36x +81=0时,得x 1=-3,x 2=-9,
∴该函数图象与x 轴的交点为(-9,0),(-3,0);
(4)∵抛物线的顶点坐标为(-6,-27),
∴当x =-6时,y 有最小值,最小值为-27;
(5)∵该函数图象与x 轴的交点为(-9,0),(-3,0),且抛物线的开口向上, ∴当-9<x <-3时,y <0.
6.已知二次函数的图象以A (-1,4)为顶点,且过点B (2,-5).
(1)求该二次函数的表达式;
(2)求该二次函数图象与y 轴的交点坐标.
解:(1)由顶点A (-1,4),可设二次函数关系式为y =a (x +1)2+4(a ≠0). ∵二次函数的图象过点B (2,-5),
∴-5=a (2+1)2+4,解得a =-1.
∴二次函数的关系式是y =-(x +1)2+4;
(2)令x =0,则y =-(0+1)2+4=3,
∴图象与y 轴的交点坐标为(0,3).
7.如图3,已知抛物线y =x 2+bx +c 经过A (-1,0),B (3,0)两点.
图3
(1)求抛物线的表达式和顶点坐标;
(2)当0<x <3时,求y 的取值范围;
(3)点P 为抛物线上一点,若S △PAB =10,求出此时点P 的坐标.
解:(1)把A (-1,0),B (3,0)分别代入y =x 2+bx +c 中,
得
∴抛物线表达式为y =x 2-2x -3.
∵y =x 2-2x -3=(x -1)2-4,
∴顶点坐标为(1,-4);
(2)由图可得当0<x <3时,-4≤y <0;
(3)∵A (-1,0),B (3,0),∴AB =4.
设P (x ,y ),则S △PAB =12
AB ·|y |=2|y |=10, ∴|y |=5,∴y =±5.
①当y =5时,x 2-2x -3=5,解得x 1=-2,x 2=4,
此时P 点坐标为(-2,5)或(4,5);
②当y =-5时,x 2-2x -3=-5,方程无解.
综上所述,P 点坐标为(-2,5)或(4,5).
8.如图4,在一面靠墙的空地上用长为24 m 的篱笆围成中间隔有二道篱笆的长方形花圃.设花圃的宽AB 为x m ,面积为S m 2.
(1)求S 与x 的函数关系式及自变量的取值范围;
(2)已知墙的最大可用长度为8 m ,
①求所围成花圃的最大面积;
②若所围花圃的面积不小于20 m 2,请直接写出x 的取值范围.
图4
解:(1)S =x (24-4x )=-4x 2+24x (0<x <6);
(2)①S =-4x 2+24x =-4(x -3)2+36,
由24-4x ≤8,24-4x >0,解得4≤x <6,
当x =4时,花圃有最大面积为32;
②令-4x 2+24x =20时,解得x 1=1,x 2=5,
∵墙的最大可用长度为8,即24-4x ≤8,
∴x ≥4,∴4≤x ≤5.
9.[2017·三原校级月考]东方小商品市场一经营者将每件进价为80元的某种小商品原来按每件100元出售,一天可售出100件.后来经过市场调查,发现这种小商品单价每降低1元,其销量可增加10件.
(1)该经营者经营这种商品原来一天可获利润__2__000__元;
(2)若设后来该小商品每件降价x 元,该经营者一天可获利润y 元.
①若该经营者经营该商品一天要获利润2 090元,求每件商品应降价多少元?
②求出y 与x 之间的函数关系式,并求出当x 取何值时,该经营者所获利润最大,且最大利润为多少元? 解:(1)若商店经营该商品不降价,则一天可获利润:100×(100-80)=2 000(元);
(2)①设该商品每件降价x 元,依题意,得(100-80-x )(100+10x )=2 090,
即x 2-10x +9=0,解得x 1=1,x 2=9.
答:每件商品应降价1元或9元;
②根据题意得y =(100-80-x )(100+10x )
=-10x 2+100x +2 000,
当x =-b 2a=5时,y 最大=2 250元, 答:该经营者所获最大利润为2 250元.
10.[2016·泰安]如图6,在平面直角坐标系中,抛物线y =ax 2+bx +c 的顶点坐标为(2,9),与y 轴交于点A (0,5),与x 轴交于点E ,B.
图6
(1)求二次函数y =ax 2+bx +c 的表达式;
(2)过点A 作AC 平行于x 轴,交抛物线于点C ,点P 为抛物线上的一点(点P 在AC 上方),作PD 平行于y 轴交AB 于点D ,问当点P 在何位置时,四边形APCD 的面积最大?并求出最大面积.
解:(1)设抛物线的表达式为y =a (x -2)2+9,
把A (0,5)代入得4a +9=5,解得a =-1,
∴y =-(x -2)2+9=-x 2+4x +5;
(2)当y =0时,-x 2+4x +5=0,
解得x 1=-1,x 2=5,∴E (-1,0),B (5,0),
设直线AB 的表达式为y =mx +n ,
把A (0,5),B (5,0)代入,得m =-1,n =5,
∴y =-x +5,
设P (x ,-x 2+4x +5),则D (x ,-x +5),PD =-x 2+4x +5+x -5=-x 2+5x ,∵AC =4,
∴四边形APCD 的面积= ,
当时,四边形APCD 的面积最大,最大面积为.
11.[2017·双台子区校级一模]如图7,在平面直角坐标系中,二次函数y =x 2+bx +c 的图象与x 轴交于A ,B (3,0)两点,与y 轴交于c (0,-3),点P 是直线BC 下方抛物线上的动点.
(1)求出二次函数的表达式;
….
图7
(2)连结PO ,PC ,并将△POC 沿y 轴对折,得到四边形POP ′C ,那么是否存在点P ,使得四边形POP ′C 为菱形?若存在,求出点P 的坐标,若不存在,请说明理由;
(3)当点P 运动到什么位置时,四边形ACPB 的面积最大?求出此时P 的坐标和四边形ACPB 的最大面积. 解:(1)把B (3,0),C (0,-3)代入y =x 2+bx +c ,
∴这个二次函数的表达式为y =x 2-2x -3;
(2)存在.理由如下:
如答图①,作OC 的垂直平分线交直线BC 下方的抛物线于点P ,垂足为点E .则PO =PC ,
∵△POC 沿CO 翻折,得到四边形POP ′C ,
∴OP ′=OP ,CP ′=CP ,∴OP ′=OP =CP ′=CP ,
∴四边形POP ′C 为菱形,∵C 点坐标为(0,-3),
∴E 点坐标为,∴点P 的纵坐标为-32, 把y =代入y =x 2-2x -3,得 x 2-2x -3=-32,解得,
∵点P 在直线BC 下方的抛物线上,
∴,
∴满足条件的点P 的坐标为
第11题答图① 第11题答图②
(3)如答图②,作PF ⊥x 轴于点F ,交BC 于点E ,BC 的表达式为y =x -3,设E (m ,m -3),P (m ,m 2-2m -3).
则PE =m -3-(m 2-2m -3)=-m 2+3m =,
S △BCP =S △BEP +S △CEP
备注:以下内容仅显示部分,需完整版请下载!











