
孝感市七校教学联盟
期末联合考试
高一数学文科试卷
本试题卷共4页,共22题。满分150分,考试时间120分钟。
注意事项:
1、请考生务必将自己的姓名、准考证号、所在学校填(涂)在试题卷和答题卡上。
2、考生答题时,选择题请用2B铅笔将答题卡上对应题目的答案标号涂黑;非选择题请按照题号顺序在各题的答题区域内作答,超出答题区域书写的答案无效。
3、考试结束后,请将本试卷和答题卡一并上交。
第I卷 选择题
一、选择题:本大题共12小题,每小题5分,共60分. 在每小题给出的四个选项中,只有一项符合题目要求. 请在答题卡上填涂相应选项.
1. 直线的倾斜角是 ( )
A. B. C. D.
【答案】C
【解析】直线的斜率为:,
直线倾斜角为,则,
所以,故选C.
2. 设且,则下列关系式正确的是( )
A. B. C. D.
【答案】D
【解析】当c=0时,显然ac=bc,故A错误;
当a>0>b时, >0>,故C错误;
当0>a>b时,,故B错误;
∵y=x3是增函数,且a>b,∴,故D正确。
故选D.
3. 若直线过圆的圆心,则实数的值为( )
A. B. 1 C. D. 3
【答案】C
【解析】圆的圆心为(-1,2).
所以,解得.故选C.
4. 在等差数列中,,,则的值是( )
A. 13 B. 14 C. 15 D. 16
【答案】A
【解析】根据等差数列的性质可知:.
所以.故选A.
5. 若实数、满足约束条件则的最小值是( )
A B. C. D. 3
【答案】B
【解析】作出不等式组对应的平面区域如图:
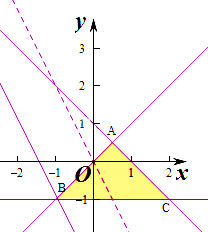
由z=2x+y得y=−2x+z,
平移直线y=−2x+z,
由图象可知当直线y=−2x+z经过点B时,直线的截距最小,
此时z最小,
由,解得,
即B(−1,−1),此时z=−1×2−1=−3,
故选:B
6. 已知是两条不重合的直线, 是不重合的平面, 下面四个命题中正确的是( )
A. 若,则 B. 若,则
C. 若, 则∥ D. 若,则∥
【答案】C
【解析】试题分析:由,是两条不重合的直线,,是不重合的平面,知:在A中:若,则与相交或平行,故A错误;在B中:若,则与相交、平行或,故B错误;在C中:若,则由面面平行的判定定理得,故C正确;在D中:若,则或,故D错误.故选:C.
考点:直线与平面之间的位置关系.
7. 若不等式的解集为,则的值是( )
A. 10 B. -10 C. 14 D. -14…
【答案】D
【解析】不等式的解集为
即方程=0的解为x=或
故
则a=−12,b=−2,a+b=−14.
故选D.
8. 在△ABC中,若,, , 则B等于( )
A. B. 或 C. D. 或
【答案】D
【解析】
9. 在正方体中,M、N分别为棱BC和棱的中点,则异面直线AC和MN所成的角为( )
A. B. C. D.
【答案】C
【解析】试题分析:连接,,∴为异面直线和所成的角,而三角形为等边三角形,∴,故选C.
考点:异面直线所成的角.
【方法点睛】本小题主要考查异面直线所成的角、异面直线所成的角的求法,考查空间想象能力、运算能力和推理论证能力,考查转化思想,属于基础题;求异面直线所成的角的方法:求异面直线的夹角关键在于平移直线,常用相似比,中位线,梯形两底,平行平面等手段来转移直线;连接,将平移到,根据异面直线所成角的定义可知为异面直线所成的角,而三角形为等边三角形,即可求出此角.
10. 一空间几何体的三视图如图所示,则该几何体的体积为( )
A. B.
C. D.
【答案】A
【解析】由三视图知该几何体是一个简单组合体,
上面是一个四棱锥,四棱锥的底面是一个正方形,对角线长是2,侧棱长是2,高是;
下面是一个圆柱,圆柱的底面直径是2,高是2,
所以该组合体的体积是.
故选A.
点睛:思考三视图还原空间几何体首先应深刻理解三视图之间的关系,遵循“长对正,高平齐,宽相等”的基本原则,其内涵为正视图的高是几何体的高,长是几何体的长;俯视图的长是几何体的长,宽是几何体的宽;侧视图的高是几何体的高,宽是几何体的宽.由三视图画出直观图的步骤和思考方法:1、首先看俯视图,根据俯视图画出几何体地面的直观图;2、观察正视图和侧视图找到几何体前、后、左、右的高度;3、画出整体,然后再根据三视图进行调整.
11. 已知圆上一点到直线的距离为,则的最小值为( )
A. 1 B. 2 C. D.
【答案】B…
【解析】圆的圆心为,半径为.
则圆心到直线的距离为.
所以.故选B.
点睛:研究圆上的动点到直线的距离的问题可转为研究圆心到直线的距离,最大距离为圆心到直线的距离加半径,最下距离为圆心到直线的距离减半径.
12. 设是各项为正数的等比数列,是其公比,是其前项的积,且,则下列结论错误的是( )
A. B.
C. 与均为的最大值 D.
【答案】D
【解析】∵是各项为正数的等比数列,q是其公比,是其前n项的积,
由可得a7=1,故B正确;
由可得a6>1,∴q=∈(0,1),故A正确;
由是各项为正数的等比数列且q∈(0,1)可得数列单调递减,
∴,故D错误;
结合,可得C正确。
故选:D.
点睛:本题主要研究的是利用等比数列的性质来研究等比数列积的变化情况,首先确定数列的正负,由条件知是正项数列后,那么积的大小关系就可以转化为项和1的大小关系.
第Ⅱ卷 非选择题
二、填空题:本题共4小题,每小题5分.请将答案填在答题卡对应题号的位置上,答错位置、书写不清、模棱两可均不得分.
13. 过点且垂直于直线的直线方程是_____________.
【答案】
【解析】直线的斜率为,则垂直于直线的直线的斜率为.
则过点且垂直于直线的直线方程:.
整理得:.
14. 以为圆心且过原点的圆的方程为_____________.
【答案】
【解析】设圆心是C,因为圆经过原点,所以半径r=,
所以圆的标准方程为.
故答案为:.
15. 长方体的长、宽、高分别为3,2,1,其顶点都在球O的球面上,则球O的表面积为_________________…
【答案】
【解析】长方体的长、宽、高分别为3,2,1,其顶点都在球O的球面上,可知长方体的对角线的长就是球的直径,
所以球的半径为:.
则球O的表面积为:.
故答案为:14π.
点睛:若长方体长宽高分别为则其体对角线长为;长方体的外接球球心是其体对角线中点.找几何体外接球球心的一般方法:过几何体各个面的外心分别做这个面的垂线,交点即为球心. 三棱锥三条侧棱两两垂直,且棱长分别为,则其外接球半径公式为: .
16. 若直线 过点,则的最小值为_________.
【答案】
【解析】 ,当且仅当 时取等号.
点睛:在利用基本不等式求最值时,要特别注意“拆、拼、凑”等技巧,使其满足基本不等式中“正”(即条件要求中字母为正数)、“定”(不等式的另一边必须为定值)、“等”(等号取得的条件)的条件才能应用,否则会出现错误.
三、解答题:本大题共6小题,满分70分,解答应写出文字说明,证明过程或演算步骤.
17. 已知的三个顶点是,,.
(1)求边上的高所在直线的方程;
(2)求边上的中线所在直线的方程.
【答案】(1);(2).
试题解析:
(1)边所在直线的斜率
因为所在直线的斜率与BC高线的斜率乘积为
所以高线的斜率为又因为BC高线所在的直线过
所以高线所在的直线方程为,即
(2)设中点为M则中点
所以BC边上的中线AM所在的直线方程为
18. 如图,在△ABC中,,,AD是BC边上的高,沿AD把△ABD折起,使.
(1)证明:平面ADB⊥平面BDC;
(2)若,求三棱锥DABC的体积 .
【答案】(1)见解析;(2).
【解析】试题分析:(1)注意折叠前后的不变量,尤其是没有变化的直角,折叠前有AD^BD,AD^CD,折叠后仍然成立,可推得AD^面BCD,进一步可得平面ABD^平面BDC;(2)由(1)可知AD为三棱锥的高,底面三角形为直角三角形,根据体积公式即可求得.
试题解析:(1)∵折起前是边上的高,…
∴当折起后,, 2分
又, ∴平面, 5分
又∵平面, ∴平面平面; 7分
(2)由(1)知,又∵,
, 10分
由(1)知,平面, 又∵
, 14分
15分
考点:面面垂直的判定,三棱锥的体积.
19. 设的内角所对应的边长分别是且
(1)当时,求的值;
(2)当的面积为3时,求的值.
【答案】(1);(2).
【解析】试题分析:(Ⅰ)因为,可得,由正弦定理求出a的值.
(Ⅱ)因为△ABC的面积,可得,再由余弦定理可得a2+c2=20=(a+c)2-2ac,由此求出a+c的值.
试题解析:
(Ⅰ)∵∴
由正弦定理可知: ,∴
(Ⅱ)∵
∴ ∴
由余弦定理得:
∴,即
则:
故:
20. 已知关于的方程:,.
(1)若方程表示圆,求的取值范围;
(2)若圆与直线:相交于两点,且,求的值.
【答案】(1);(2).
【解析】试题分析:(Ⅰ)关于x,y的方程x2+y2-2x-4y+m=0可化为(x-1)2+(y-2)2=-m+5,可得-m+5>0,即可求m的取值范围;
(Ⅱ)求出圆心到直线的距离,利用勾股定理,即可求m的值.
试题解析:
(1)方程可化为 , …
显然 时方程表示圆.
(2)圆的方程化为,
圆心,半径,
则圆心到直线l: 的距离为
.
∵,∴,有 ,
∴
得
【答案】生产A种产品2吨,B种产品2吨,该企业能够产生最大的利润.
【解析】试题分析:根据已知条件列出约束条件,与目标函数利用线性规划求出最大利润.
试题解析:
设生产A种产品x吨、B种产品y吨,能够产生利润z元,目标函数为
由题意满足以下条件:
可行域如图
平移直线,由图可以看出,当直线经过可行域上的点M时,截距最大,即z最大.
解方程组得M的坐标为x=2,y=2.
所以zmax=10000x+5000y=30000.
故生产A种产品2吨,B种产品2吨,该企业能够产生最大的利润.
点睛:线性规划的实质是把代数问题几何化,即数形结合的思想.需要注意的是:一、准确无误地作出可行域;二、画标准函数所对应的直线时,要注意与约束条件中的直线的斜率进行比较,避免出错;三、一般情况下,目标函数的最大或最小会在可行域的端点或边界上取得.
22. 已知等差数列的前项和为,且,.
(1)求数列的通项公式;
(2)若数列满足,,记数列的前项和为,证明:.
【答案】(1) ;(2)见解析.
【解析】试题分析:(1)利用等差数列的通项公式与求和公式即可得出.
(2)利用“裂项求和”方法即可得出.
试题解析:
(1)设等差数列的首项为,公差为.
∵ ,,∴
解得 …
∴ .
(2)∵ , ∴
备注:以下内容仅显示部分,需完整版请下载!











