高二年级期中质量调查数学试题(文科)
第Ⅰ卷(选择题 共40分)
一、选择题(本大题共10小题,每小题4分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.要描述一个学校的组成情况,应选用
A.工序流程图 B. 组织结构图 C. 知识结构图 D.程序框图
2.在线性回归模型中,分别选择了4个不同的模型,它们的相关指数依次为,其中回归效果最好的模型的相关指数为
A. B. C. D.
3.若为虚数单位,则等于
A. B. C. D.
4.下面是一个列联表
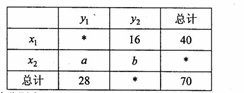
则表中处的值分别为
A. B. C. D.
5.若,则下列不等关系成立的是
A. B. C. D.
6.设,则的大小关系为
A. B. C. D.
7.已知变量与正相关,且由观测数据算得样本平均数,则由该数据算得的线性回归方程只可能是下列选项中的
A. B.
C. D.
8.阅读右边的程序框图,当该程序运行后,输出的S的值是
A. 35 B. 63 C. 84 D. 165
9.已知,设,则的值为
A. B. C. D.
10.设计算得,观察上述结果,可推测一般结论为
A. B.
C. D.
第Ⅱ卷(非选择题 共60分)
二、填空题:本大题共5小题,每小题5分,共20分.
11.已知为虚数单位,的实部与虚部互为相反数,则的值为 .
12.用反证法证明命题“如果,那么”时,假设的内容是 .
13.在成立的条件下,若,则表示把结论“成立”错判成“不成立”的概率不会超过 .
14.若则 .
15.已知函数的恰有一个零点在内,则实数的取值范围是 .
三、解答题:本大题共5小题,共40分.解答应写出文字说明、证明过程或演算步骤.
16.(本小题满分6分)
已知,求证:
17.(本小题满分8分)
计算下列各题:
(1)
(2)
18.(本小题满分8分)
求证:
19.(本小题满分8分)
对某产品的产量与成本进行分析后,得到如下数据:
|
产量/千件 |
2 |
3 |
5 |
6 |
|
成本/万元 |
6 |
7 |
8 |
11 |
(1)在下面给定的坐标系中画出表中数据的散点图;
(2)求出关于的线性回归方程并在(1)的坐标系中画出回归直线.
20.(本小题满分10分)
如图,在三棱锥中,平面,为的中点,为的中点,
(1)求证:平面
(2)求证:
备注:以下内容仅显示部分,需完整版请下载!











